原文：Hybrid Particle Filter–Particle Swarm Optimization Algorithm and Application to Fuzzy Controlled Servo Systems | IEEE Journals & Magazine | IEEE Xplore

智能优化算法课程的汇报要求，找了一篇PSO算法相关的看看，Intro部分也写得挺详细，对元启发式算法（进化）有个概述。慢慢写着，之前课上代课的老师讲了他做的大规模优化问题也有点意思，也许之后会写一下。

简介

元启发式算法

元启发式算法（metaheuristic algorithm），也称自然启发算法（nature-inspired algorithms）或进化算法（evolutionary algorithms, EAs）。

这里的”进化“指的是将类似于生物进化的一些过程如繁殖、突变、重组和选择等概念用到优化问题中。进化算法的一个优势在于它有能力跳出局部最优而寻找全局最优，但进化算法在特定类的问题上也不能保证给出全局最优。

主要工作

如作者总结，文章的主要工作有二：

1. 提出了一种新的混合元启发式算法（hybrid metaheuristic algorithm）粒子过滤-群算法（PF-PSO）
2. 在用于伺服系统的位置控制的比例积分的模糊控制器的最优调谐中应用PF-PSO算法

PF-PSO算法

PF – PSO背后的思想结合了两个算法：用于移动机器人定位的粒子滤波算法（PF）和粒子群优化算法（PSO）。

这种合并用随机生成的粒子种群取代了群体运动学的定义

算法的流程图如下：

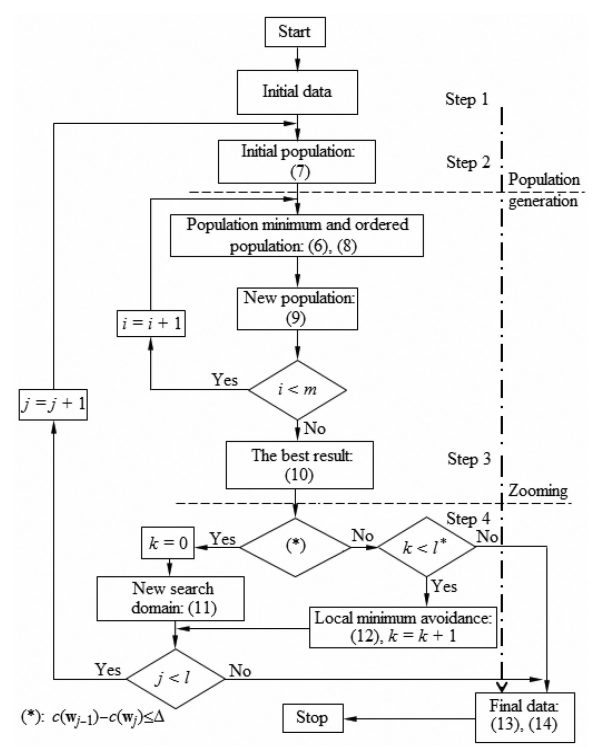
基本定义

优化问题就是要找到在一个搜索域 $D\subset \mathbb{R} ^{d_s}$（ $d_s$ 为搜索域的维度）中最小化（或最大化）代价函数 的最优点 $c:D\rightarrow \mathbb{R} ^{d_s}$，即

$$\mathbf{x}^*=\mathrm{arg}\min_{x\in D} c(\mathbf{x})$$

一个第 $k$ 代 $n$ 维（包含 个粒子/元素）的粒子群 定义为如下离散集合：

$$P_k=\{x_1,x_2,...,x_n\}$$

粒子群的表现 由每个元素的代价函数计算得到：

$$pf\left( P_k \right) =\left\{ y_1,y_2,...,y_n \right\} =\left\{ c\left( x_1 \right) ,c\left( x_2 \right) ,...,c\left( x_n \right) \right\}$$

粒子群最小就是该粒子群 中使得代价函数最小的粒子 $x_{k}^{*}$ .

一个第 $k$ 代的有序粒子群 $\tilde{P}_k$ 定义为粒子群中粒子按代价函数值大小从小到大的顺序排序的集合：

$$\tilde{P}_k=\{\tilde{x}_1,\tilde{x}_2,...,\tilde{x}_n\}$$

其中 $c(\tilde{x}_1)\le c(\tilde{x}_2)\le ...\le c(\tilde{x}_n)$.

Step 1 初始化算法参数

• $c$：代价函数（cost function）
• $D$：搜索域（search domain）
• $n$：粒子群维度（population dimension or the number of particles also called agents）
• $m$：每次缩放需要经过的粒子群代数/最大迭代次数（the number of populations generated for each zooming and also the maximum number of iterations）
• $S_N>0$：从有序粒子群中采样的方差（the variance of normal distribution in random selection (sampling)）
• $S_{Z,1}>0$：正态噪声的初始方差（the initial variance of normal distribution in noise definition）
• $\rho_1>0$：初始邻域半径（the initial vicinity radius）
• $\alpha_\rho>1$：邻域半径的缩放因子（the zooming factor for vicinity radius）
• $\alpha_z>1$：正态噪声的缩放因子（the zooming factor for normal distribution in noise definition）
• $l$：缩放的次数（the number of zooms）
• $l^*$：跳出局部最优的最大尝试次数（the maximum number of local minimum avoiding trials）
• $\Delta>0$：两次连续的缩放直接的表现差异（the relative performance between two consecutive zooms）

Step 2 迭代产生粒子群

根据参数，进行 $i=1,2,...,m$ 次迭代生成，$i=1$ 即第一代从搜索域的均匀分布中产生：

$$P_1=\mathrm{uni}_{\mathrm{rand}}\left( D_1,n \right)$$

每代生成计算粒子群的表现，存储最好的结果：

$$U=\left\{ x_{k}^{*}\mid x_{k}^{*}=\mathrm{arg}\min_{x_i\in P_k} c\left( x_i \right) ,k=1,...,m \right\}$$

同时得到有序粒子群 $\tilde{P}_k$ .

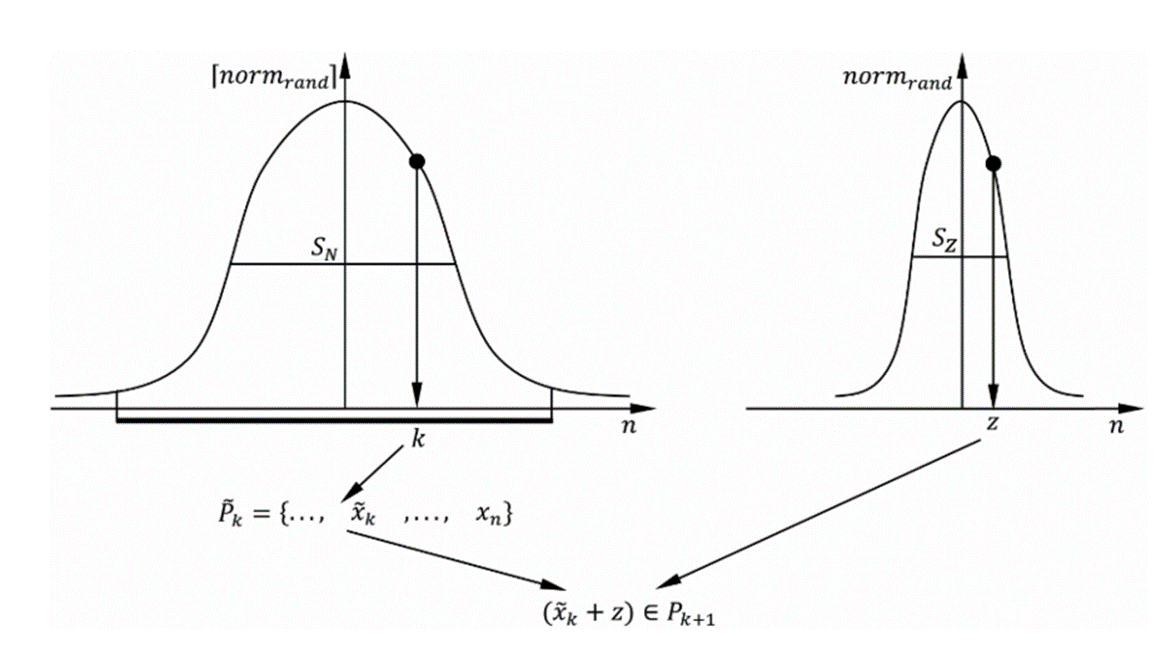
$i\ge2$，即第二代之后新的粒子群通过如下的采样得到：

$$\begin{aligned} &P_k=\left\{ \mathbf{x}_i\mid \mathbf{x}_i=\widetilde{\mathbf{x}}_{\left. \left. \lceil \mathrm{norm} _{\mathrm{rand}}\left( 0,S_N \right) \right. \right. \rceil}+\mathrm{norm}_{\mathrm{rand}}\left( 0,S_{Z,j} \right) \right.\\ &\left. \widetilde{\mathbf{x}}_{\left[ \mathrm{norm} _{\mathrm{rand}}\left( 0,S_N \right) \right.}\in \widetilde{P}_{k-1},i=1,...,m \right\}\\ \end{aligned}$$

其中，$\left. \left. \lceil \mathrm{norm}_{\mathrm{rand}}\left( 0,S_N \right) \right. \right. \rceil$ 表示以0为均值，$S_N$ 为方差的正态随机方式采样有序粒子群中的元素索引，所以离粒子群最优更近的元素更容易被保留。$\left. \mathrm{norm}_{\mathrm{rand}}\left( 0,S_{Z,j} \right) \right.$ 是一个用于产生新的粒子的正态分布。

Step 3 存储最优结果

在第二步中经过 $m$ 次迭代我们得到了一个每代的最优结果集合 $U$，在进行搜索域缩放之前我们要存储这个集合中的最优值，算法总共需要进行 $l$ 次搜索域缩放，所以我们需要存储 $l$ 次，即：

$$W=\left\{ w_j\mid w_j=\mathrm{arg}\min_{x_i\in U} c\left( x_i \right) ,j=1,...,l \right\}$$

根据两代之间代价函数最优值的差异，就可以在缩放的时候决定是进一步减小搜索域还是扩大搜索域以跳出局部最优。

Step 4 缩放搜索范围

根据参数，进行 $j=1,2,...,l$ 次搜索域缩放，每次缩放完成后回到 Step 2 重新生成粒子群迭代。

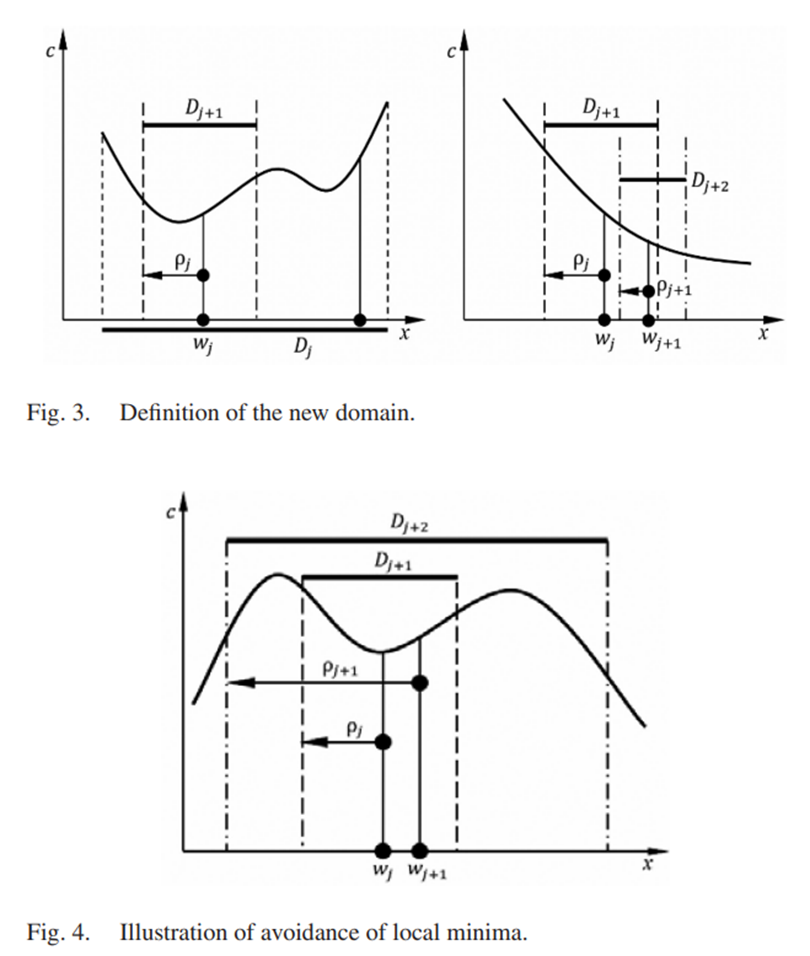
如果 $c\left( w_{j-1} \right) -c\left( w_j \right) \le \Delta ,k<l$，新的搜索域变为：

$$D_{j+1}=V\left( w_j,\rho _j \right) \cap D$$

其中 $V\left( w_j,\rho _j \right)$ 是以 $w_j$ 为中心半径为 $\rho_j$ 的邻域。同时 $k$ 重置为0。

这个邻域和由于下一轮粒子群生成的随机分布的方差由下面的公式缩小：

$$\rho _{j+1}=\frac{\rho _j}{\alpha _{\rho}},S_{Z,j+1}=\frac{S_{Z,j}}{\alpha _Z}$$

如果 $c\left( w_{j-1} \right) -c\left( w_j \right) >\Delta ,k<l,k<l^*$，新的搜索域同样变为：

$$D_{j+1}=V\left( w_j,\rho _j \right) \cap D$$

同时 $k=k+1$ .

邻域和用于下一轮粒子群生成的随机分布的方差由下面的公式放大：

$$\rho _{j+1}=\alpha _{\rho}\rho _j,S_{Z,j+1}=\alpha _ZS_{Z,j}$$

终止条件

1. 经过 $l$ 次搜索域缩放，即进行了 $l\times m$ 轮粒子迭代生成。

2. 如果次连续的缩放直接的表现差异 $c\left( w_{j-1} \right) -c\left( w_j \right) \le \Delta$ 的同时已经进行了 $l^*$ 次避免局部最小（扩大搜索域）的操作。

   满足以上条件中的一个算法就会终止，输出得到的最优点和最优代价函数：

   $$x^*=\omega _j,c(x^*)=c(\omega _j)$$