前言

对于一个可靠的系统来说，面对未知输入/类别的时候如果进行错误的操作/分类是有风险的。然而大多数真实数据本质上都是动态的，且真实数据是不可预测的。

所以一个可靠的系统必须能够忽略或拒绝未知输入/类别或设计连续检测新的输入并对未知输入执行某些操作的处理机制。 最理想的情况下，系统需要在不间断的输入数据流中标记未知输入并添加新检测到的对象作为要学习的新类别。 e.g. 自动驾驶。

传统的分类模型都是在一个封闭世界假设下进行训练，即假设测试数据和训练数据都来自同样的分布（称作“分布内”,in-distribution, ID）。模型应当如何去处理这些不属于训练分布的样本（即分布外, out-of-distribution, OOD），这也是开放世界领域所关注的问题。

增量学习(Incremental Learning, IL)，也称持续学习、终身学习。主要标准是学习过程的顺序性质，一次只能使用来自一个或几个任务的一小部分输入数据。主要挑战是要求学习时不会发生灾难性遗忘：随着新任务或领域的添加，先前学习的任务或领域的表现不应随着时间的推移而显着下降。这是神经网络中一个更普遍的问题的直接结果，即稳定性-可塑性困境。

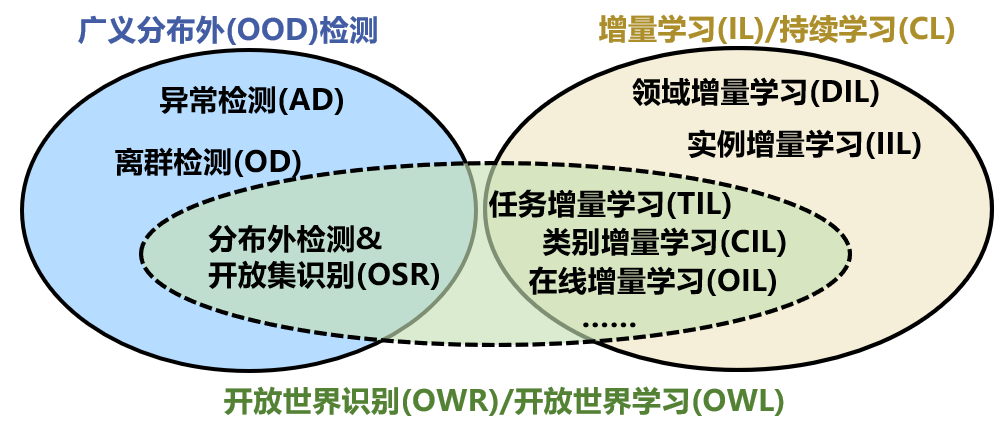
开放世界识别的定义

一个开放世界识别方法应该包含以下三个部分：

1. 多类别的开放集识别函数 ​F(x) 以及一个 新颖性检测器 ​v\left( \varphi \right)
   OSR ≈ Novelty-detection + multi-class recognition
2. 标注过程 ​L\left( x \right)
3. 增量学习函数 ​I_t\left( \varphi ;Dt \right)

OWR也称为开放世界学习(OWL)[4] 在OOD综述文献[1]中OWR也被作者定义为新颖性检测+增量学习

开放集风险

开放空间：​\displaystyle \mathcal{O}=S_o-\bigcup_{i\in N}B_r(x_i)
开放空间风险：​\displaystyle R_{\mathcal{O}}(f_y)=\frac{\int_{\mathcal{O}}f_y(x)dx}{\int_{S_o}f_y(x)dx}
开放集风险：​\displaystyle \operatorname*{argmin}_{f\in\mathcal{H}}\left\{R_{\mathcal{O}}(f)+\lambda_rR_{\mathcal{E}}(f)\right\}

test