Logo

菜单

【论文】树结构策略梯度的大规模交互式推荐系统

Dymay
Dymay
发布于 2025-09-02 / 12 阅读
0
0

【论文】树结构策略梯度的大规模交互式推荐系统

原文：[1811.05869] Large-scale Interactive Recommendation with Tree-structured Policy Gradient

解决交互式推荐系统 (Interactive Recommender Systems, IRS) 中可推荐的物品（例如，电影、音乐、新闻）数量巨大时，传统的强化学习 (RL) 方法低效的问题。提出了一种名为 TPGR (Tree-structured Policy Gradient Recommendation) 的框架

传统的推荐系统通常是静态的，一次性生成一个推荐列表 。而交互式推荐系统 (IRS) 则不同，它会与用户进行连续的互动：系统推荐一个物品，用户给出反馈（如点击、评分、跳过），系统根据这个反馈来调整下一步的推荐策略 。

问题

真实的推荐场景中，物品库里的物品数量（即“动作空间”的大小 |A|）通常是成千上万甚至数百万的 。

  • 基于价值的RL方法 (如 DQN): 这类方法需要计算出在状态 s 下，每一个可能动作 a 的Q值（预期回报），然后选择 Q 值最大的那个动作，即 \arg\max_{a\in A}Q(s,a) 。当动作空间 巨大时，遍历所有动作来找最大值是极其耗时的，甚至不可行 。

  • 基于策略的RL方法 (如 DDPG): 类似地，很多DDPG的变种在决策时也需要对所有物品进行一次打分和排序，来挑出最优的推荐项，其决策时间复杂度同样与动作空间的大小呈线性关系 。

有研究尝试将离散的物品映射到一个连续的向量空间中，然后让策略网络输出一个连续向量，再通过K近邻 (KNN) 查找最近的真实物品作为推荐 。但这种方法存在一个“不一致性”问题：训练策略网络时用的目标是连续向量，而实际与环境交互并产生反馈的却是离散物品，这种偏差可能导致学习过程出错 。

TPGR模型

TPGR的核心思想是将整个物品集合（动作空间）构建成一棵平衡的层次化聚类树 (balanced hierarchical clustering tree) 。将一次性的、困难的大决策，分解为多步的、简单的小决策 。

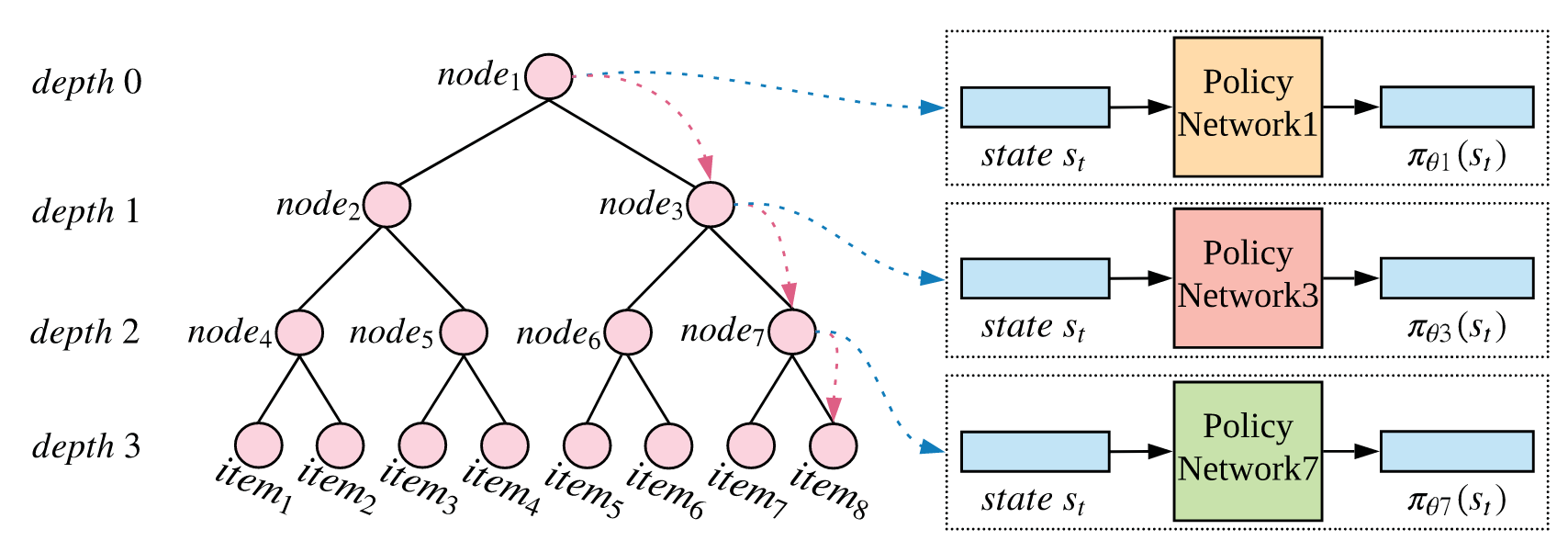
  • 在这棵树中，每个叶子节点唯一对应一个真实的可推荐物品 。

  • 推荐一个物品的过程，就转变成了从树的根节点开始，通过一系列决策，最终走到某个叶子节点的过程 。

  • 在每个非叶子节点上，都有一个独立的、小型的策略网络，负责决定下一步该往哪个子节点走 。

通过这种方式，原本需要在 |A| 个物品中选择一个的复杂问题，变成了一个深度为 d、每步最多只有 c 个选项的决策序列。这极大地降低了决策的复杂度 。

树构建

首先目标是构建一棵平衡的层次化聚类树。所谓“平衡”，是指树中每个节点的子树高度最多只差一 。为了实现和表达方便，论文进一步要求每个非叶子节点（除了叶节点的父节点外）拥有相同数量的子节点，记为 c，称之为分支因子 (branching factor)。

聚类方法: 论文采用了自顶向下 (divisive) 的聚类方法 。从包含所有物品的根节点开始，重复地将一个节点内的物品集合分裂成 c 个大小尽量均等的子集（即子节点），直到每个节点只包含一个物品为止 。论文中用了 K-means-based 和 PCA-based 两种具体的聚类算法。

物品表示: 聚类算法需要对物品进行向量化表示。论文用了三种表示方法：

  • Rating-based: 直接使用用户-物品评分矩阵中，该物品对应的那一列作为其向量表示 。

  • VAE-based: 使用变分自编码器 (VAE) 将高维的评分向量压缩成一个低维稠密向量 。

  • MF-based: 使用矩阵分解 (MF) 技术学习出每个物品的低维潜向量 。

树的深度 d、分支因子 c 和物品总数 |A| 之间存在如下关系：

c^{d-1}\lt|A|\le c^d

如果预先设定了树的深度 d，则可以计算出每层需要的的分支数

\begin{equation}c=\lceil|A|^{1/d}\rceil\end{equation}

树状策略学习

树构建好后，就需要学习在每个非叶子节点上的决策策略。每个非叶子节点 v 都关联一个策略网络 π_{θ_v} 。这个网络接收当前的用户状态 s 作为输入，输出一个概率分布，表示从节点 v 走向其每个子节点的概率 。

文章用REINFORCE 算法来训练所有策略网络的参数 θ。目标函数策略梯度的目标是最大化期望的累积折扣奖励 J(π_θ)：

J(π_θ)= \mathbb{E}_{\pi_\theta}\left[\sum_{t=1}^n\gamma^{t-1}r_t\right]


其中 n 是一个推荐序列的长度。根据策略梯度定理，目标函数对参数 θ 的梯度可以近似为：

\begin{equation}\nabla_\theta J(\pi_\theta)\approx\mathbb{E}_{\pi_\theta}\left[\nabla_\theta\log\pi_\theta(a|s)Q^{\pi_\theta}(s,a)\right]\end{equation}

这里的 Q^{π_θ}(s,a) 是在状态 s 执行动作 a 后，遵循策略 π_θ 所能获得的期望累积回报。在实际计算中，它通常用一次完整的序列采样（Monte Carlo rollout）得到的实际回报来估计，即：

\hat{Q}^{\pi_\theta}(s_t,a_t)=\sum_{i=t}^n\gamma^{i-t}r_i

这就是从时间步 t 开始到序列结束的所有未来折扣奖励之和。

在TPGR中，选择一个物品（动作）a_t 对应于在树上走过一条从根到叶的路径 p_t 。这条路径由 d 步决策构成。因此，在状态 s_t 下选择动作 a_t 的总概率，是这条路径上每一步决策概率的乘积：

\begin{equation}\pi_\theta(a_t|s_t)=\prod_{d^{\prime}=1}^d\pi_{\theta_{i_{d^{\prime}}}}(p_{td^{\prime}}|s_t)\end{equation}

其中，p_{td'} 是在路径的第 d' 步选择的子节点，θ_{i_{d'}} 是该步所在父节点的策略网络参数。

由于每个非叶子节点的策略网络参数是独立的，对整体参数 θ 的梯度，可以分解为对路径上每个相关策略网络参数的梯度之和。对数似然的梯度因此变为：

\begin{equation}\nabla_\theta\log\pi_\theta(a_t|s_t)=\nabla_\theta\sum_{d^{\prime}=1}^d\log\pi_{\theta_{i_{d^{\prime}}}}(p_{td^{\prime}}|s_t)\end{equation}

结合以上几点，在采集到一个完整的推荐序列后，对参数 θ 的更新规则为：

\Delta\theta=\nabla_\theta\log\pi_\theta(a_t|s_t)\cdot\hat{Q}^{\pi_\theta}(s_t,a_t)\\ \theta\leftarrow\theta+\eta\Delta\theta

TPGR框架的核心优势在于效率，这体现在其时间和空间复杂度上。

复杂度分析

时间复杂度：

  • 标准RL方法: \mathcal{O}(|A|)，因为需要评估每一个动作 。

  • TPGR: 决策过程包含 d 步，每一步从 c 个子节点中选择一个。每个策略网络的计算复杂度是 \mathcal{O}(c)。因此，总的时间复杂度是：

\mathcal{O}(d\times c)\approx\mathcal{O}(d\times |A|^{1/d})

由于树层数 d 通常较小，这个复杂度远低于: \mathcal{O}(|A|)，实现了显著的效率提升。

空间复杂度：

  • 标准RL方法: 通常是一个大型网络，其输出层的大小为 |A|，所以空间复杂度为 \mathcal{O}(|A|)。

  • TPGR: 需要存储树中所有非叶子节点的策略网络。非叶子节点的总数 \mathcal{I} 约等于：

\begin{equation}\mathcal{I}=1+c+c^2+\cdots+c^{d-1}=\frac{c^d-1}{c-1}\end{equation}

每个网络的空间复杂度是 \mathcal{O}(c)。因此，总的空间复杂度为：

\begin{equation}\mathcal{O}(\mathcal{I}\times c)\approx\mathcal{O}\left(\frac{c^d}{c}\times c\right)=\mathcal{O}(c^d)\end{equation}

因为 c^d≈|A|，所以TPGR的空间复杂度约为 \mathcal{O}(|A|)，与标准方法在同一量级 。

【知识】偏差-方差分解的推导

评论