参考:
https://nndl.github.io/
【Bias Variance Decomposition 偏差-方差分解 详解】 https://www.bilibili.com/video/BV1Cu411w7o5/?share_source=copy_web&vd_source=0261fe4cd89b81ec3bc903ee7677db61
《神经网络与深度学习》笔记3 - 偏差方差分解(详细证明) - 知乎
比较基础的一个点,整理一下,也是NNDL习题2-10的推导
如何在模型的拟合能力和复杂度之间取得一个较好的平衡,对一个机器学习算法来讲十分重要。偏差-方差分解(Bias-Variance Decomposition) 是一个很好的分析和指导工具。
以回归问题为例,假设样本的真实分布为 p_r(x,y) ,并采用平方损失函数,模型 f(x) 的期望错误为
\mathcal{R}(f)=\mathbb{E}_{(x,y)\sim p_r(x,y)}\left[\left(y-f(x)\right)^2\right]
那么最优的模型为
f^*(x)=\mathbb{E}_{y\sim p_r(y|x)}[y]
其中 p_r(y|x) 为样本的真实条件分布,f^*(x) 为使用平方损失作为优化目标的最优模型,其损失为
\varepsilon=\mathbb{E}_{(x,y)\sim p_r(x,y)}\left[\left(y-f^*(x)\right)^2\right]
损失 \varepsilon 通常是由于样本分布以及噪声引起的,无法通过优化模型来减少。期望错误可以分解为
\begin{aligned}\mathcal{R}(f)&=\mathbb{E}_{(x,y)\sim p_{r}(x,y)}\left[\left(y-f^{*}(x)+f^{*}(x)-f(x)\right)^{2}\right]\\&=\mathbb{E}_{x\sim p_{r}(x)}\left[\left(f(x)-f^{*}(x)\right)^{2}\right]+\varepsilon\end{aligned}\tag{1}
其中第一项是当前模型和最优模型之间的差距,是机器学习算法可以优化的真实目标。在实际训练一个模型 f(x) 时,训练集 D 是从真实分布 p_r(x,y) 上独立同分布地采样出来的有限样本集合。不同的训练集会得到不同的模型。令 f_D(x) 表示在训练集 D 上学习到的模型,一个机器学习算法(包括模型以及优化算法)的能力可以用不同训练集上的模型的平均性能来评价:
\begin{aligned}\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-f^{*}(\mathbf{x})\right)^{2}\right]&=\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]+\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]-f^{*}(\mathbf{x})\right)^{2}\right]\\&=\red{\left(\mathbb{E}_{D}\left[f_{D}(\mathbf{x})-f^{*}(\mathbf{x})\right]\right)^{2}}+\blue{\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]\right)^{2}\right]}\end{aligned}
其中第一项为偏差(Bias),是指一个模型在不同训练集上的平均性能和最优模型的差异,可以用来衡量一个模型的拟合能力。第二项是方差(Variance),是指
一个模型在不同训练集上的差异,可以用来衡量一个模型是否容易过拟合。
推导过程如下:
\begin{aligned}&\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]+\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]-f^{*}(\mathbf{x})\right)^{2}\right]\\=&\blue{\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]\right)^{2}\right]}+
\mathbb{E}_{D}\left[\left(f^*(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\right)^2\right]\\
&+2\mathbb{E}_{D}\{\left[f_D(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\right]\cdot\left[\mathbb{E}_{D}
[f_D(\mathbf{x})]-f^*(\mathbf{x})\right]\}\\
\end{aligned}
对于第三项中 \mathbb{E}_{D}\{\left[f_D(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\right]\cdot\left[\mathbb{E}_{D}
[f_D(\mathbf{x})]-f^*(\mathbf{x})\right]\} ,展开,根据期望定义显然可以得到均为0:
\begin{aligned}&\mathbb{E}_{D}\{\green{f_D(\mathbf{x})\mathbb{E}_{D}[f_D(\mathbf{x})]}-f_D(\mathbf{x})f^*(\mathbf{x})-\green{\mathbb{E}_{D}^2[f_D\mathbf(x)]}+f^*(\mathbf{x})\mathbb{E}_{D}[f_D(\mathbf{x})]\}\\
=&\mathbb{E}_{D}\{\green{\mathbb{E}_{D}[f_D(\mathbf{x})]]\cdot[f_D(\mathbf{x})-\mathbb{E}_{D}[f_D(\mathbf{x})]]}\}-\mathbb{E}_{D}\{f^*(\mathbf{x})\cdot[f_D(\mathbf{x})-\mathbb{E}_{D}[f_D(\mathbf{x})]]\}\\
=&0 +0 =0
\end{aligned}
此处不完全展开另一种方法是可以考虑 f_D(\mathbf{x}) 与 f^*(\mathbf{x}) 是相互独立(前者是通过具体的数据集学习到而后者是理想最优模型)且 \mathbb{E}_D[f_D(\mathbf{x})] 显然与 D 无关,所以可以直接将两个乘积项的期望拆成两个期望的乘积:
\mathbb{E}_{D}\{f_D(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\}\cdot\mathbb{E}_{D}\{\mathbb{E}_{D}
[f_D(\mathbf{x})]-f^*(\mathbf{x})\}=0
而前一项根据期望定义为0所以整体为0
所以有
\begin{aligned}&\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]+\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]-f^{*}(\mathbf{x})\right)^{2}\right]\\=&\blue{\mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-\mathbb{E}_{D}\left[f_{D}(\mathbf{x})\right]\right)^{2}\right]}+
\mathbb{E}_{D}\left[\left(f^*(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\right)^2\right]
\end{aligned}
上式中的第二项 \mathbb{E}_{D}\left[\left(f^*(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\right)^2\right] ,我们令 X=f^*(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})] 利用结论 \mathbb{E}(X^2)=\mathbb{E}^2(X)+Var(X)=\mathbb{E}^2(X)+\mathbb{E}[(X-\mathbb{E}(X))^2] 并可以验证 Var(X)=0
此处直观理解可以考虑 \mathbb{E}_{D}
[f_D(\mathbf{x})] 是模型的平均表现, 与某一训练集 D 的分布无关 , f^*(\mathbf{x}) 是最优模型, 同样与 D 分布无关, 所以可以直接去掉期望,也即 Var(X)=0
则有
\mathbb{E}_{D}\left[\left(f^*(\mathbf{x})-\mathbb{E}_{D}
[f_D(\mathbf{x})]\right)^2\right]=\red{\left(\mathbb{E}_{D}\left[f_{D}(\mathbf{x})-f^{*}(\mathbf{x})\right]\right)^{2}}
证毕。
用 \mathbb{E}_{D}\left[\left(f_{D}(\mathbf{x})-f^{*}(\mathbf{x})\right)^{2}\right] 来代替公式(1)中的 \left(f(x)-f^{*}(x)\right)^{2} ,期望错误可以进一步写为
\begin{aligned}\mathcal{R}(f)&=\mathbb{E}_{x\sim p_{r}(x)}\left[\mathbb{E}_{\mathcal{D}}\left[\left(f_{\mathcal{D}}(x)-f^{*}(x)\right)^{2}\right]\right]+\varepsilon\\&=\red{\left(\mathrm{bias}\right)^2}+\blue{\mathrm{variance}}+\varepsilon\end{aligned}
最小化期望错误等价于最小化偏差和方差之和(可以理解为泛化误差)。
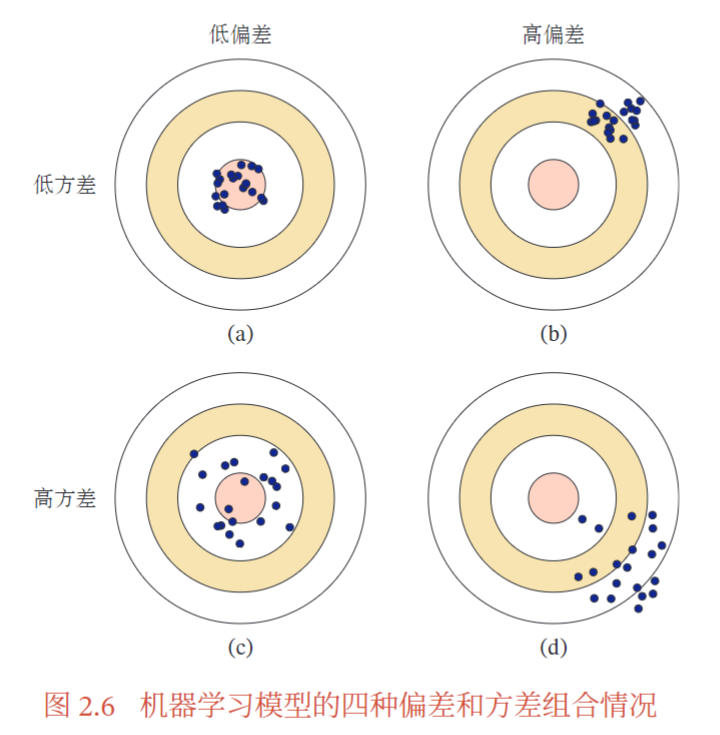
(a) 理想情况,方差和偏差都比较低
(b) 为高偏差低方差的情况,表示模型的泛化能力很好,但拟合能力不足
(c) 为低偏差高方差的情况,表示模型的拟合能力很好,但泛化能力比较差,当训练数据比较少时会导致过拟合
(d) 为高偏差高方差的情况,是一种最差的情况
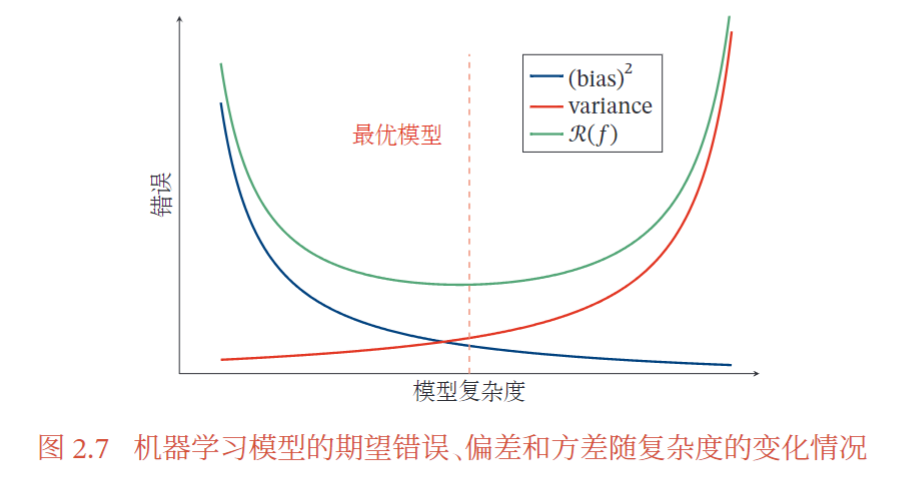
方差一般会随着训练样本的增加而减少 。当样本比较多时,方差比较少,这时可以选择能力强的模型来减少偏差。然而在很多机器学习任务上,训练集往往都比较有限,最优的偏差和最优的方差就无法兼顾。随着模型复杂度的增加 ,模型的拟合能力变强,偏差减少而方差增大 ,从而导致过拟合。所以结构正则化通过控制模型复杂度进而减小方差,但会导致偏差上升,正则化参数过大也会导致整体的期望错误增大。
一般来说,当一个模型在训练集上的错误率比较高时,说明模型欠拟合,偏差比较高 。这种情况可以通过增加数据特征、提高模型复杂度、减小正则化系数 等操作来改进。
当模型在训练集上的错误率比较低,但验证集上的错误率比较高时,说明模型过拟合,方差比较高 。这种情况可以通过降低模型复杂度、加大正则化系数、引入先验等 方法来缓解。
此外,还有一种有效降低方差的方法为集成模型,即通过多个高方差模型的平均来降低方差。