Reading list: GitHub - kaize0409/Awesome-Graph-OOD
以节点分类为例来定义分布变化下图学习的节点级任务。我们考虑三种不同的问题场景（即图 OOD 泛化、训练时图 OOD 适应和测试时图 OOD 适应），如图所示。
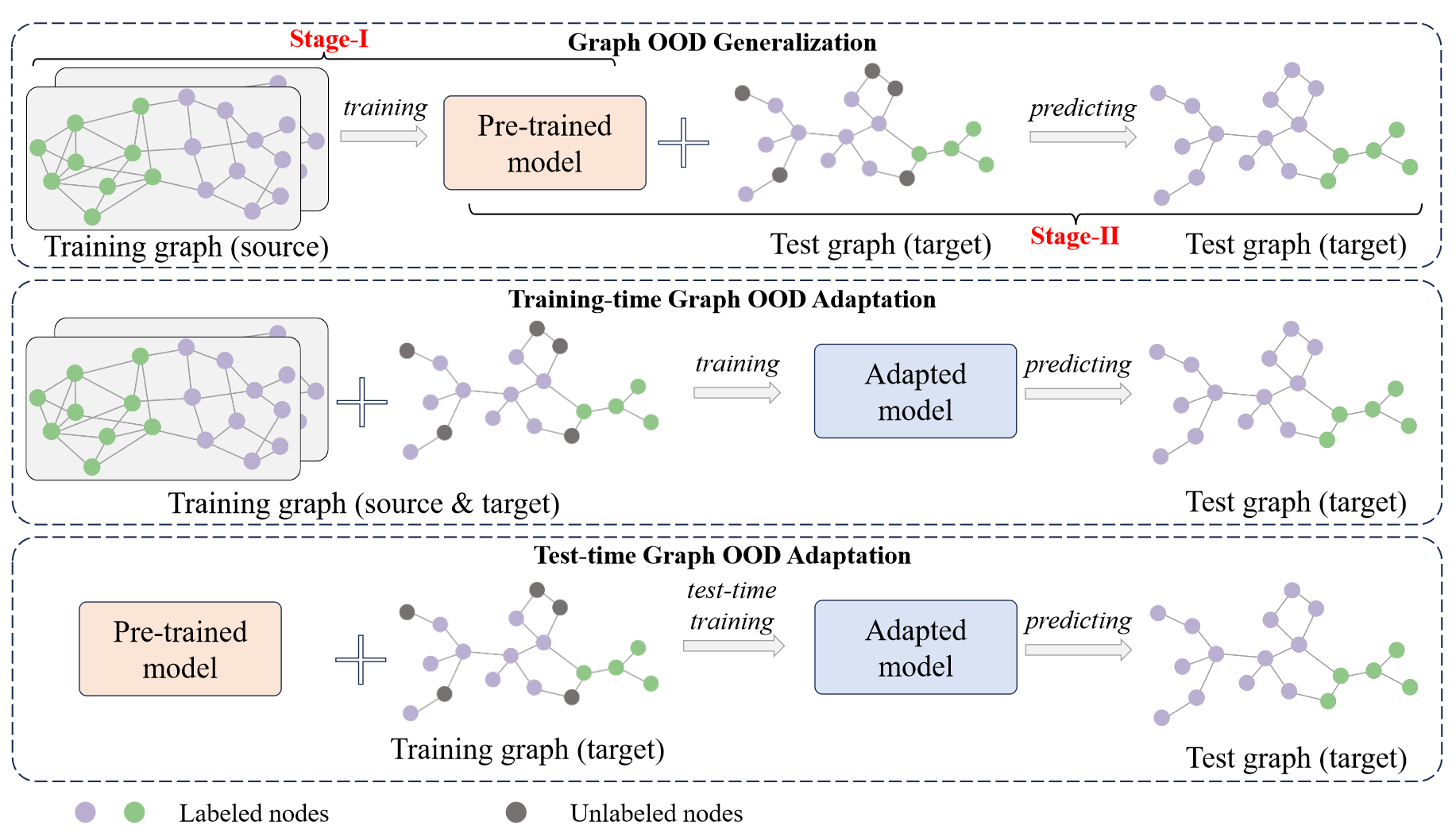这些定义可以轻松扩展以涵盖边缘级别和图形级别的学习任务。
文章提出的方法分类，每个场景都是按照基于模型和基于数据来分：
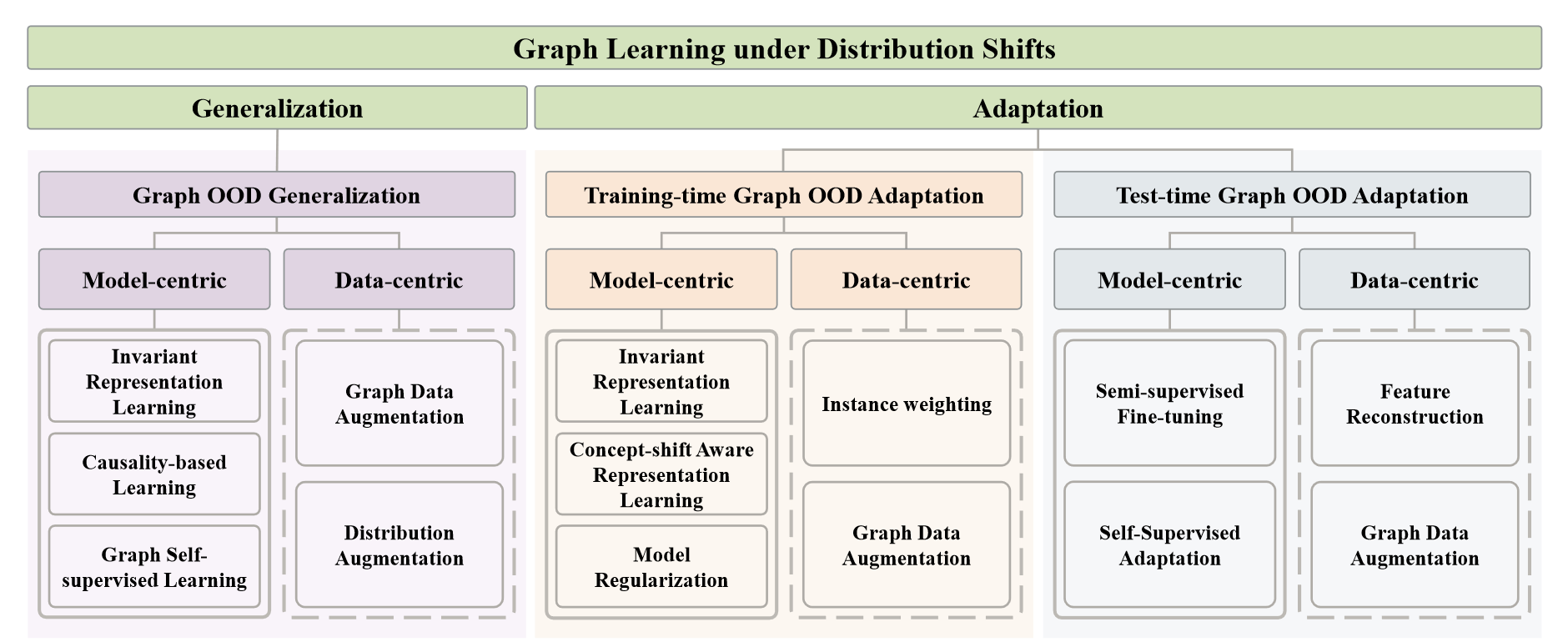这里主要关注一下域适应领域中的训练阶段图OOD适应和测试阶段图 OOD 适应。（这两者符合图域适应的定义）
训练阶段图OOD适应
基于模型的方法
用于训练时间图 OOD 适应的以模型为中心的方法可以进一步分为不变表示学习和概念转移感知表示学习，其目的是学习分布对齐的表示，以及模型正则化，其重点是通过模型正则化实现有效的知识迁移。
不变表示学习
技术在训练时图 OOD 适应中的目标是学习跨源图和目标图的不变表示，确保对分布变化的鲁棒性，可参考【论文】学习分布外泛化的不变图表示 - Dymay 理解。该技术经常用于协变量假设下的域适应，其中潜在表示和标签之间的不变关系
受理论泛化界限的启发，域不变表示学习方法旨在训练图编码器 g(\cdot) 以最小化诱导的边缘源分布 P_S(\boldsymbol{H}) 和目标分布 P_T(\boldsymbol{H}) 之间的差异，同时也识别潜在空间中的分类器 f(\cdot)，以最小化经验源风险。为了实现这两个目标，域不变表示学习的损失函数可以表述如下：
其中 l_{\text {reg }} 表示有利于诱导边缘分布 P(\boldsymbol{H}) 对齐的正则化项。主要采用三种策略：
分布距离最小化
分布距离最小化直接采用边缘分布之间的距离正则化项。方法在距离度量的选择以及它们旨在对齐的具体表示方面有所不同。 SR-GNN 将中心矩差异视为正则化，并对齐传统 GCN 最后一层的分布差异。 CDNE、GraphAE 和 GRADE 的目标是最小化所有潜在层的源和目标之间的统计差异，其中正则化项是不同层的分布距离的总和。就距离度量而言，CDNE 使用边际最大均值差异和类条件边际最大均值差异，GraphAE 将最大均值差异的多核变体视为距离度量，GRADE 定义并利用子树差异。 JHGDA 依靠分层池模块来提取网络层次结构，并通过边际和类条件最大平均差异的指数形式最小化层次表示中的统计差异。
对于不可训练的表示，例如 SimpleGCN 中的潜在嵌入，SR-GNN 应用实例加权技术。在这种方法中，使用核均值匹配来优化可学习的权重参数，以减轻分布差异。 HC-GST 使用伪标签，结合异性比率和标签准确性来对齐分布，并通过核均值匹配优化可学习权重。最近，DREAM 采用互补分支（图级和子图增强）并强制它们之间的一致性，以减轻有偏见的伪标签并减少分布差异。此外，SelMAG 通过选择信息丰富的源图并调整嵌入和分类空间，利用元学习进行精确的子图和节点选择来提高可转移性，从而设计了一种基于传输的最佳算法。对抗性学习
对抗性学习。对抗性学习方法通过训练图编码器 g(\cdot) 生成混淆域鉴别器 f_d(\cdot) 的嵌入来对齐表示。相应地，正则化项通常表示为 g(\cdot) 和 f_d(\cdot) 之间的极小极大博弈，如下所示：\min _{f_d} \max _g l\left(f_d(g(\mathbf{A}, \mathbf{X})), \mathbf{Y}_d\right)其中 \mathbf{Y}_d 表示域标签，损失函数可以选择负距离损失，或域分类损失。除了将其视为极小极大问题外，DANE 还探索使用两种对称和对抗性损失进行模型训练，旨在实现双向传输。通常，对抗性对齐发生在最终的隐藏层中，但 GraphAE 除外，它对齐所有隐藏层中的表示。此外，值得注意的是，SGDA 还通过采用加权自监督伪标签损失来考虑源图的标签稀缺问题。 SDA 研究开放集设置下的问题，利用基于熵的分离策略将目标节点分类为特定组和不确定组，并通过对抗性学习技术专门对齐特定组中的节点。最近，JDA-GCN 引入了联合对抗域自适应图卷积网络，通过结构图对齐利用局部和全局图结构，提高模型捕获图数据中复杂依赖关系的能力
解纠缠表示学习
解纠缠表征学习将表征分成不同的、信息丰富的因素。在这些因素中，其中一个因素旨在捕获对于目标任务（例如分类）至关重要的领域不变特征。这种领域不变的组件在不同领域保持一致，以保留与分类相关的语义信息，从而促进有效的适应。并且可以选择性地操纵解开的组件以满足目标任务的特定要求。解纠缠表示学习的损失函数可以定义为：\min _{f, g_s} \mathbb{E}_{\mathbf{A}, \mathbf{X}, \mathbf{Y}}\left[l\left(f\left(g_s(\mathbf{A}, \mathbf{X})\right), \mathbf{Y}\right)\right]+\min _{g_s, g_o}\left(l_{\text {reg }}+l_{\text {recon }}+l_{\text {add }}\right)其中 g_s 表示用于获取不变任务相关信息的图编码器， g_o 表示除 g_s 之外的其他组件的图编码器，l_{\text {reg }} 表示用于增强不同组件之间的分离的正则化项，l_{\text {recon }} 表示旨在恢复从串联表示中恢复原始图结构，从而防止信息丢失。引入了附加术语 l_{\text {add }} ，以促进解缠结表示的学习，使特定组件能够表现出所需的特性。在 ASN 中，表示被分解为域私有部分和域不变分类相关部分。另外还添加了域对抗性损失，以促进不变表示的学习。与 DIVA 类似，DGDA 假设图生成过程由域不变语义潜变量、域潜变量和随机潜变量独立控制。为了学习具有所需特征的表示，域分类损失和噪声重建损失被视为附加损失。
概念转移感知表示学习
最近的一些工作超越了协变量假设，并考虑了跨领域的标签函数的变化。当 P(\boldsymbol{Y}|\boldsymbol{X}) 或 P(\boldsymbol{Y}|\boldsymbol{H}) 存在概念偏移（参考【知识】领域泛化及其理论基础 - Dymay），即标签函数发生变化时，上界中的不可估计适应性项可能很大，并且以前的不变表示学习方法在目标上的性能不再得到保证。 [5]中提供的类似上限和示例说明了基于协变量移位假设的不变表示学习方法的不足。为了进一步适应标签函数的变化，SRNC 利用图同质性，结合一个稳健的分类 GNN 模块和一个无监督聚类 GNN 模块来减轻联合分布 P(\boldsymbol{Y},\boldsymbol{H}) 中的分布变化。值得注意的是，SRNC 还能够处理测试数据中出现新类的开放集设置。在 StruRW 中，通过自适应调整源图中边的权重来识别和减轻条件结构偏移 P(\boldsymbol{A}|\boldsymbol{Y}) 。在此基础上，Pair-Align 被提议作为 StruRW 的扩展，以解决条件结构移位和标签移位问题。此外，朱等人证明，在上下文随机块模型中，与输入特征空间 P(Y|H) 中的条件移位相比，GCN 中的图异质性和图卷积会加剧潜在空间 P(Y|H) 中的条件移位。 X）。因此，他们引入了 GCONDA，通过 Wasserstein 距离正则化显式匹配跨域的 P(Y|H) 分布，此外，他们还提出了 GCONDA++，共同最小化 P(Y|H) 和 P(H) 的差异。
基于数据的方法
侧重于利用和增强图数据本身来提高适应性能。通过考虑图的独特特征，这些方法可以有效地解决分布变化带来的复杂性。两种突出的以数据为中心的技术是实例加权和图数据增强。
实例加权
实例加权为数据点分配不同的权重，是传统迁移学习中常用的以数据为中心的技术。训练阶段图 OOD 适应方法中也采用了类似的图实例加权策略，包括针对特定任务或目的的边加权、节点加权和图加权。 Ye 等人借鉴了 Adaboost 和 TrAda 的想法。将实例加权技术用于边缘符号预测任务。每次迭代中都会调整边权重，减少分配给错误分类的不同源实例的权重，以减轻图之间的分布变化。另一方面，刘等人认识到原始数据和带有伪标签的增强数据之间的分布变化可能会阻碍自训练的有效性，因此建议根据信息增益重新加权增强节点实例，以缩小原始分布之间的差距和移动的分布。在多源传输设置中，源图对于目标图的预测可能并不同样重要，并且其中一些可能质量较差。为了解决这些挑战，RSS-GCN 和NESTL 都采用图加权技术来有效地组合可用的源图。 NES-TL 提出 NES 索引来定量测量两个图之间的结构相似性，并使用基于 NES 的分数作为权重来集成在每个源图的实例和标记的目标实例上训练的弱分类器。另一方面，RSS-GCN 利用强化学习来选择高质量的源图，旨在最小化所选源图和目标图之间的分布差异。这种样本选择策略可以看作是一种特殊的二元实例权重
图数据增强
与上述加权策略不同，一些工作深入探索图数据增强策略以减轻分布变化，主要集中在边缘自适应。董等人发现边缘预测中的数据集移位挑战是由于训练中存在链接而测试中缺乏链接观察而引起的。为了解决这个问题，他们提出了 FakeEdge，这是一种基于子图的链接预测框架，可以有意添加或删除子图中的焦点链接。这种方法旨在解耦边缘的双重角色，既充当表示学习的组成部分，又充当链接预测的标签。毕等人。将领域级知识转移问题重新考虑为学习样本知识增强后验分布。他们首先从源图和目标图中学习样本的相似性，并在每个样本与其相似样本之间建立桥梁，其中包含有价值的预测知识。然后采用 GNN 模型在构建的桥接图上跨源样本和目标样本传输知识。最近，引入了一种称为 DC-GST 的新颖框架，以桥接自训练中增强训练实例和测试实例之间的分布变化，该框架结合了分布变化感知边缘预测器，以提高模型分配的泛化性伪标签，以及精心设计的伪标签选择标准。此外，LTLP 通过解决链路预测中公共邻居的长尾分布来增强图数据增强，通过高质量边缘生成和表示细化有效地增加尾节点对的公共邻居
测试阶段图 OOD 适应
基于模型的方法
微调是一种广泛使用的方法，用于在测试期间调整预训练模型。然而，如何有效利用预训练模型中的信息会是一个挑战，通常可以通过以下两种技术来解决：
半监督微调
在这种技术中，模型通常以无监督的方式进行预训练，以编码更多可转移和可概括的结构信息。随后，在微调过程中，会合并与任务相关的和特定领域的信息。这里的一个显着挑战是目标图中标签的稀缺，这可能导致过度拟合。为了避免负迁移，GAdapter 和 AdapterGNN 都采用参数高效微调（PEFT）策略，该策略采用瓶颈结构，通过减小可调参数的大小来减轻过度拟合。或者，GraphControl 考虑自适应地集成目标信息，合并两个组件：以邻接矩阵作为输入的冻结预训练模型和以基于节点特征的核矩阵作为输入的可训练副本。这两个组件通过具有扩展参数的零 MLP 连接，旨在减轻目标节点特征中的噪声，同时逐渐将下游信息集成到预训练模型中。 PROGRAM 通过两个关键组件在测试数据和原型之间建立强大的连接：原型图模型，通过利用原型和测试数据之间的关系生成可靠的伪标签，以及强大的自训练模块，迭代地细化这些伪标签通过一致性正则化。
自监督适应
在该技术中，任务相关信息被编码到预训练模型中，随后在目标图上执行无监督微调任务。然而，这种无监督任务中出现了一个重大挑战：模型可能会失去对主要任务的区分能力或可能学习不相关的信息。为了解决这个问题，人们提出了各种技术来保留模型的判别力。 SOGA 和 GAPGC 采用基于信息的设计策略，而 GT3 通过有意的架构设计和额外的正则化约束来应对挑战。在 SOGA 中，Mao等人利用最大化模型输入和输出之间的互信息的损失来增强辨别能力，而 GAPGC 采用对抗性伪群体对比策略来解决过度自信偏差并减轻捕获风险冗余信息，从信息瓶颈角度对与主任务相关的信息有下界保证。另一方面，GT3 将模型构造为包括两个共享初始层的分支：一个主任务（分类）分支和一个自监督分支，并且在测试期间仅调整自监督分支，以便可以保持主要任务分支的辨别能力。此外，它还集成了训练和测试输出嵌入之间的额外正则化约束，从而增强了它们的统计相似性并避免了大幅波动。其他相关研究，例如 GTOT-Tuning（在测试期间跨任务传输知识）和 GraphGLO（将可共享组件直接合并到模型中）也为解决测试时适应期间的分布变化提供了宝贵的见解。
基于数据的方法
测试时图 OOD 适应中以数据为中心的方法侧重于修改输入数据，以有效解决训练域和目标域之间的分布变化。这些方法强调图特征的重建和增强，以在不改变预先训练的架构的情况下增强模型的性能。特征重建。特征重建旨在通过重建目标图的节点特征以类似于测试期间源图的节点特征来减轻训练和目标之间的分布变化。在 FRGNN 中，Ding 等人。 [151]考虑半监督节点分类任务，并利用 MLP 建立预训练 GNN 的输出和输入空间之间的映射。随后，使用编码的 one-hot 类向量作为输入，MLP 生成类代表表示。通过用相应类的代表性表示替换标记测试节点的特征，并通过消息传递将更新的信息传播到其他未标记测试节点，预计可以减轻测试节点和训练节点之间的图嵌入偏差。
图形数据增强。除了重建特征之外，Jin 等人。 [18]引入了一个名为 GTRANS 的图转换框架来解决测试期间的分布变化。图变换被建模为对图结构和节点特征注入扰动，并随后通过无参数代理损失进行优化。还提供理论分析来指导选择适当的替代损失函数。在GTRANS的基础上，GraphCTA[15]进一步考虑协同集成模型自适应和图自适应。协作循环是通过使用节点邻域的预测来适应模型、通过邻域对比学习增强图、然后将适应的图重新引入模型适应过程而形成的。此外，SGOOD 框架 [152] 利用与任务无关的子结构，通过将它们的关系编码为有效的表示来增强图级 OOD 检测。值得强调的是，这种以数据为中心的测试时图 OOD 适应方法优先考虑调整测试数据而不是测试数据。在处理大规模预训练模型时，修改预训练模型尤其有益。