迁移学习问题考虑源域和目标域存在不同的分布:P_s(\boldsymbol{x},y)\ne P_t(\boldsymbol{x},y)
显然由于目标域标签不可获取无法直接去衡量这种联合分布的差异,所以根据
将问题进行各种转化。
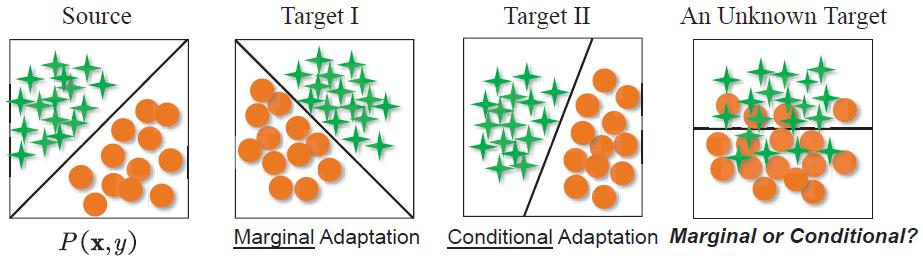
迁移学习方法也可根据转化的方式大致分为:
边缘分布自适应(MDA)
即认为差异主要来自于边缘分布:P_s(\boldsymbol{x})\ne P_t(\boldsymbol{x})
假设:P_s(y|\boldsymbol{x})\approx P_t(y|\boldsymbol{x})
本质与自变量漂移(偏移)相同,所以对联合分布差异的衡量也主要考虑边缘分布的差异:D(P_s(\boldsymbol{x},y),P_t(\boldsymbol{x},y))\approx D(P_s(\boldsymbol{x}),P_t(\boldsymbol{x}))条件分布自适应(CDA)
即认为差异主要来自于条件分布:P_s(y|\boldsymbol{x})\ne P_t(y|\boldsymbol{x})
假设:P_s(\boldsymbol{x})\approx P_t(\boldsymbol{x})
对联合分布差异的衡量主要考虑条件分布的差异:D(P_s(\boldsymbol{x},y),P_t(\boldsymbol{x},y))\approx D(P_s(y|\boldsymbol{x}),P_t(y|\boldsymbol{x}))
联合分布自适应(JDA)
同时考虑边缘分布和条件分布差异,通过两中分布距离之和来近似联合分布距离:D(P_s(\boldsymbol{x},y),P_t(\boldsymbol{x},y))\approx D(P_s(y|\boldsymbol{x}),P_t(y|\boldsymbol{x}))+D(P_s(\boldsymbol{x}),P_t(\boldsymbol{x}))动态分布自适应(DDA)
以不同重要程度考虑边缘分布和条件分布差异,即加入一个平衡因子 \mu:D(P_s(\boldsymbol{x},y),P_t(\boldsymbol{x},y))\approx \mu D(P_s(y|\boldsymbol{x}),P_t(y|\boldsymbol{x}))+(1-\mu)D(P_s(\boldsymbol{x}),P_t(\boldsymbol{x}))
从结构风险最小化(SRM)出发,迁移学习方法的统一表征可以表示为:
其中
\boldsymbol{v}\in\mathbb{R}^{N_s} 为源域样本的权重,v_i\in[0,1]。
T 为作用于源域和目标域上的特征变换函数。
此处用 1/N_s 计算均值,但显式地引入权重后也要变为加权均值,具体方式并不统一。
第二项可以称为迁移正则化项。根据该公式可以派生出三大类迁移学习方法,也可以同时结合考虑:
样本权重迁移法
目标是学习源域样本的权重 \boldsymbol{v}。基本思想是从源域中通过权重选出足够有代表性的子集,并且和目标域的相似度最大。特征变化迁移法
保持源域样本权重 \boldsymbol{v}=\bold{1},目标是学习一个特征变换 T 来减小正则化项。即让变换后的源域目标域的分布差异最小。
特征变换法大致有两类:统计特征变换:显式地最小化源域和目标域分布差异求解。如直接用KL散度、JS散度和互信息等分布距离度量。
几何特征变换:从几何分布出发,隐式求解分布差异。如生成对抗网络中的判别器就是一种隐式距离衡量标准。
模型预训练迁移法
保持源域样本权重 \boldsymbol{v}=\bold{1},R(T(\mathcal{D}_s),T(\mathcal{D}_t)):=R(\mathcal{D}_T;f_s),目标是如何将源域的判别函数 f_s 对目标域数据进行正则化和微调。
当存在一个已经在源域训练好的模型,并且目标域有一些可供学习的标签时,可以直接进行微调。

