【知识】注意力机制

参考：神经网络与深度学习 (nndl.github.io)

注意力机制

用 \boldsymbol{X}=\left[\boldsymbol{x}_1, \cdots, \boldsymbol{x}_N\right] \in \mathbb{R}^{D \times N} 表示组输入信息，其中 D 维向量 \boldsymbol{x}_n\in\mathbb{R}^D 表示一组输入信息。为了节省计算资源，不需要将所有信息都输入神经网络，只需要从 \boldsymbol{X} 中选择一些和任务相关的信息。注意力机制的计算可以分为两步：

1. 在所有输入信息上计算注意力分布

2. 根据注意力分布来计算输入信息的加权平均

为了从 N 个输入向量中选择出和某个特定任务相关的信息，我们需要引入一个和任务相关的表示，称为查询向量（Query Vector），并通过一个打分函数来计算每个输入向量和查询向量之间的相关性。给定一个和任务相关的查询向量 \boldsymbol{q}，查询向量 \boldsymbol{q} 可以是动态生成的，也可以是可学习的参数。

我们用注意力变量 𝑧 ∈ [1, 𝑁] 来表示被选择信息的索引位置，即 𝑧 = n 表示选择了第 n 个输入向量。为了方便计算，我们采用一种“软性”的信息选择机制。首先计算在给定 \boldsymbol{q} 和 \boldsymbol{X} 下，选择第 n 个输入向量的概率 \alpha_n，

其中 \alpha_n 称为注意力分布（Attention Distribution），s\left(\boldsymbol{x}, \boldsymbol{q}\right) 为注意力打分函数，可以使用以下几种方式来计算：

• 加性模型：s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{v}^{\top} \tanh (\boldsymbol{W x}+\boldsymbol{U q})

• 点积模型：s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top}\boldsymbol{q}

• 缩放点积模型：\displaystyle s(\boldsymbol{x}, \boldsymbol{q})=\frac{\boldsymbol{x}^{\top}\boldsymbol{q}}{\sqrt{D}}

• 双线性模型：s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top}\boldsymbol{W q}

其中 \boldsymbol{W},\boldsymbol{U},\boldsymbol{v} 为可学习的参数，D 为输入向量的维度。

加性模型和点积模型的复杂度差不多，但是点积模型在实现上可以更好地利用矩阵乘积，从而计算效率更高；当输入向量的维度 D 比较高时，点积模型的值通常有比较大的方差，从而导致 Softmax 函数的梯度会比较小，缩放点积模型可以较好地解决这个问题；双线性模型是一种泛化的点积模型，假设 \boldsymbol{W}=\boldsymbol{U}^{\top}\boldsymbol{V}，双线性模型可以写为 s(\boldsymbol{x}, \boldsymbol{q})=\boldsymbol{x}^{\top}\boldsymbol{U}^{\top}\boldsymbol{V q}=(\boldsymbol{U x})^{\top}(\boldsymbol{V q})，即分别对 \boldsymbol{x} 和 \boldsymbol{q} 进行线性变换后计算点积。相比点积模型，双线性模型在计算相似度时引入了非对称性。

注意力分布 \alpha_n 可以解释为在给定任务相关的查询 \boldsymbol{q} 时，第 n 个输入向量受关注的程度。

软性注意力

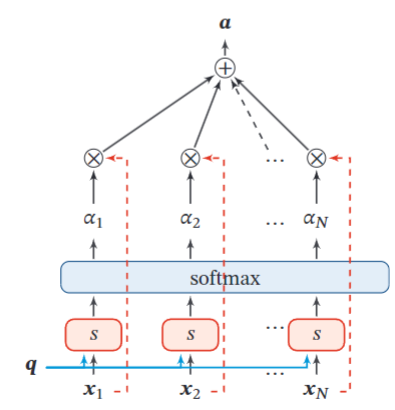
如图采用软性注意力机制（Soft Attention Mechanism）对输入信息进行汇总，

即简单将 \alpha_n 作为对应输入向量的权重求和得到输出。

硬性注意力

硬性注意力机制（Hard Attention Mechanism）有两种实现方式：

1. 选取最高概率的一个输入向量，即 \mathrm{att}(X,q)=x_{\hat{n}}，其中 \hat{n}=\underset{n}{\operatorname*{\arg\max}}\alpha_{n}

2. 通过在注意力分布式上随机采样的方式实现

硬性注意力的缺点是基于最大采样或随机采样的方式来选择信息，使得最终的损失函数与注意力分布之间的函数关系不可导，无法使用反向传播算法进行训练。因此，硬性注意力通常需要使用强化学习来进行训练，为了使用反向传播算法，一般使用软性注意力来代替硬性注意力。

键值对注意力

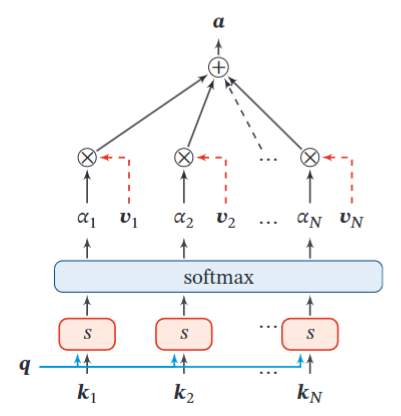
如图，更一般地可以用键值对（key-value pair）格式来表示输入信息，其中“键”用来计算注意力分布，“值”用来计算聚合信息。用 (\boldsymbol{K},\boldsymbol{V})=[(\boldsymbol{k}_1,\boldsymbol{v}_1),\cdots,(\boldsymbol{k}_N,\boldsymbol{v}_N)] 表示 N 组输入信息，给定任务相关的查询向量 \boldsymbol{q} 时，注意力函数为

当 K=V 时，键值对模式就等价于普通的软性注意力机制。

多头注意力

多头注意力（Multi-Head Attention）是利用多个查询 \boldsymbol{Q}=[\boldsymbol{q}_{1},\cdots,\boldsymbol{q}_{M}]，来并行地从输入信息中选取多组信息．每个注意力关注输入信息的不同部分。

其中 \oplus 表示向量拼接。

结构化注意力

在之前介绍中，我们假设所有的输入信息是同等重要的，是一种扁平（Flat）结构，注意力分布实际上是在所有输入信息上的多项分布。但如果输入信息本身具有层次（Hierarchical）结构，比如文本可以分为词、句子、段落、篇章等不同粒度的层次，我们可以使用层次化的注意力来进行更好的信息选择。此外，还可以假设注意力为上下文相关的二项分布，用一种图模型来构建更复杂的结构化注意力分布。

自注意力模型

对于不同的输入长度，其连接权重的大小也是不同的，所以为了提高模型处理变长输入序列的能力，可以利用注意力机制来“动态”地生成不同连接的权重，这就是自注意力模型（Self-Attention Model）

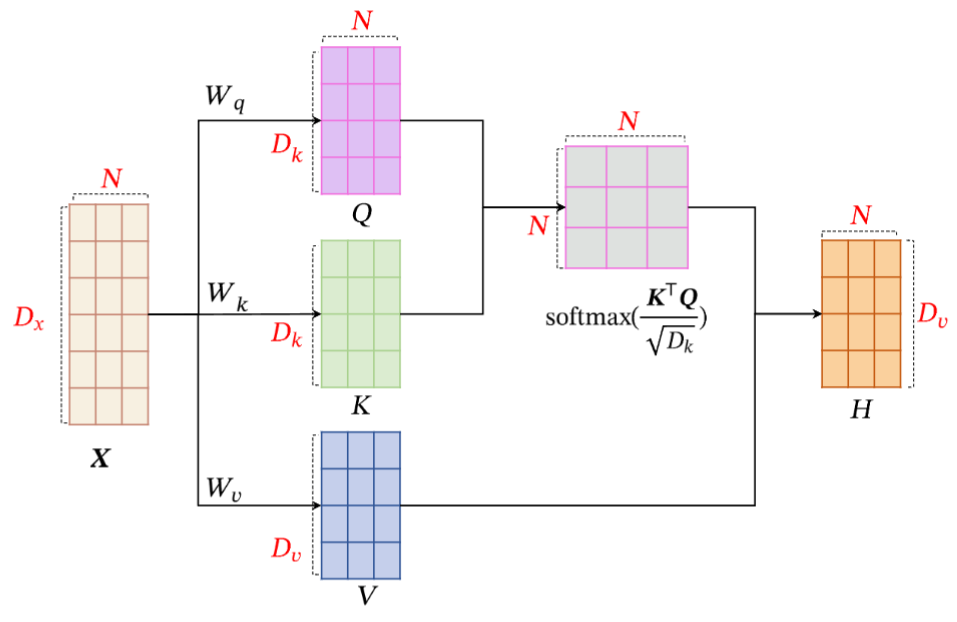假设输入序列为 \boldsymbol{X}=\left[\boldsymbol{x}_1, \cdots, \boldsymbol{x}_N\right] \in \mathbb{R}^{D \times N}，输出序列为 \boldsymbol{H}=\left[\boldsymbol{h}_1, \cdots, \boldsymbol{h}_N\right] \in \mathbb{R}^{D_v \times N}，自注意力模型的具体计算过程如下：

1. 对于每个输入 \boldsymbol{x}_i，我们首先将其线性映射到三个不同的空间，得到查询向量 \boldsymbol{q}_i\in\mathbb{R}^{D_k}、键向量 \boldsymbol{k}_i\in\mathbb{R}^{D_k} 和值向量 \boldsymbol{v}_i\in\mathbb{R}^{D_v}。对于整个输入序列 \boldsymbol{X}，线性映射过程简写为

   \begin{aligned} & \boldsymbol{Q}=\boldsymbol{W}_q \boldsymbol{X} \in \mathbb{R}^{D_k \times N} \\ & \boldsymbol{K}=\boldsymbol{W}_k \boldsymbol{X} \in \mathbb{R}^{D_k \times N} \\ & \boldsymbol{V}=\boldsymbol{W}_v \boldsymbol{X} \in \mathbb{R}^{D_v \times N} \end{aligned}

   其中 \boldsymbol{W} 为对应线性映射的参数矩阵，\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}分别是由查询向量、键向量和值向量构成的矩阵。

2. 对于每一个查询向量 \boldsymbol{q}_n\in\boldsymbol{Q}，利用键值对注意力机制，可以得到输出向量 \boldsymbol{h}_n：

   \begin{aligned} \boldsymbol{h}_n&=\operatorname{att}\Big((\boldsymbol{K},\boldsymbol{V}),\boldsymbol{q}_n\Big)\\ & =\sum_{j=1}^N \alpha_{n j} \boldsymbol{v}_j \\ & =\sum_{j=1}^N \operatorname{softmax}\left(s\left(\boldsymbol{k}_j, \boldsymbol{q}_n\right)\right) \boldsymbol{v}_j \end{aligned}

   其中 𝑛, 𝑗 ∈ [1, 𝑁] 为输出和输入向量序列的位置，\alpha_{nj} 表示第 𝑛 个输出关注到第 j 个输入的权重。

自注意力模型计算的权重 \alpha_{ij} 只依赖于 \boldsymbol{q}_i 和 \boldsymbol{k}_j 的相关性，而忽略了输入信息的位置信息。因此在单独使用时，自注意力模型一般需要加入位置编码信息来进行修正。自注意力模型可以扩展为多头自注意力（Multi-Head Self-Attention）模型，在多个不同的投影空间中捕捉不同的交互信息。

带位置编码的自注意力模型

参考：位置编码 at main · wdndev/llm_interview_note · GitHub

不同于RNN、CNN等模型，对于Transformer模型这类基于自注意力的模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此大体有两个选择：

1. 想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；

2. 想办法微调Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。