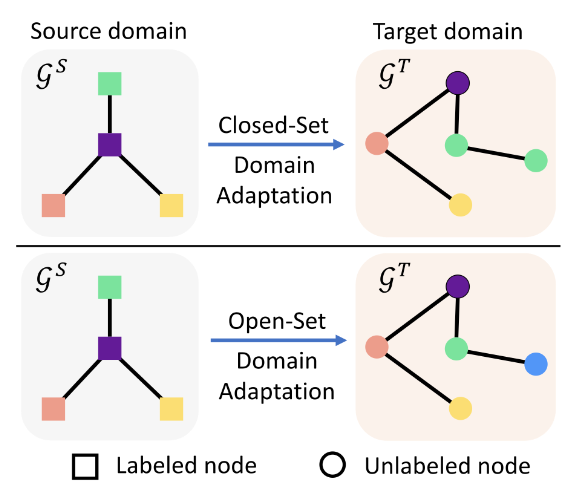
考虑如图的闭集和开放集图域适应之间的问题（节点级）设置差异。不同的颜色代表不同的类别。
具体方法如下图：
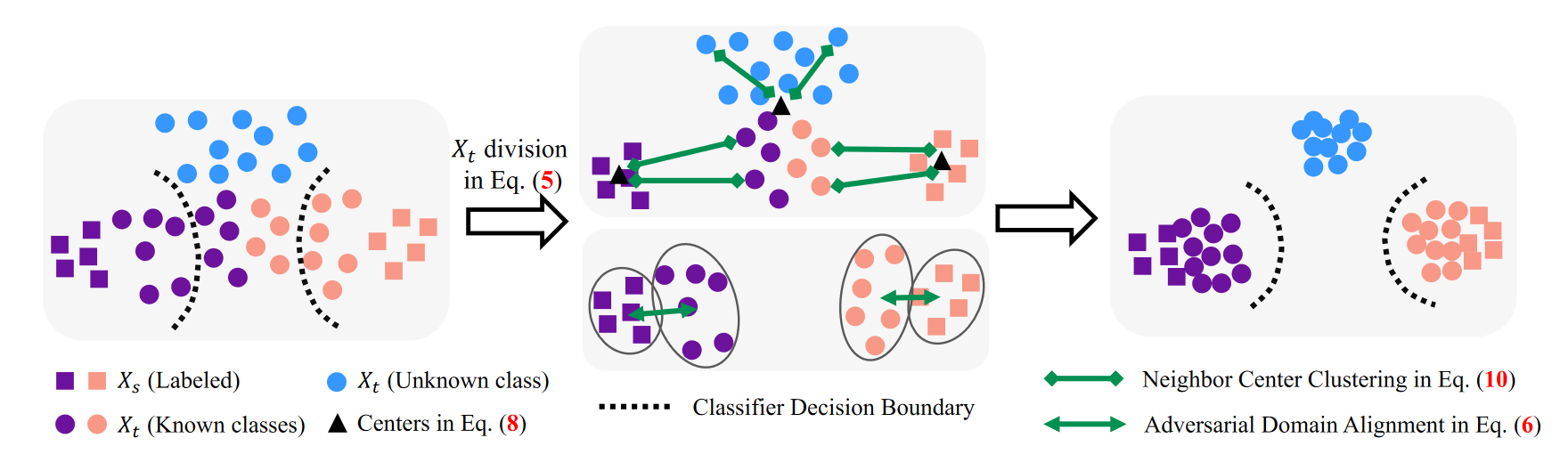采用熵作为评估分类器预测不确定性的度量。熵值越低表示预测确定性越高。具有较低熵值的目标节点更倾向于属于已知标签空间 C，而具有较高熵值的目标节点更有可能来自未知标签空 \bar{C} 。利用阈值 \gamma 自适应地将目标节点分为两组，即确定组和不确定组，利用熵 e_t=H(f_t)，其中 H(f_t)=-\sum_{i=1}^{|C_s|}{f_{t}^{i}}\log\mathrm{(}f_{t}^{i})，如下：
\gamma 设置为 \displaystyle \frac{\log \left( |C_s| \right)}{2}，其中 |C_s| 表示源类的数量，\log \left( |C_s| \right) 是分类器的最大熵值。
对于来自组 Group_c 的目标节点，这些节点很可能属于已知标签空间 C。我们利用对抗性域对齐来学习来自 的节点的域不变嵌入。具体来说，目标函数为：
域鉴别器 O(\cdot ) 尝试识别源节点和目标节点，而嵌入提取器 G(\cdot ) 旨在欺骗域鉴别器。整体流程是：
在模型训练过程中，对于来自不确定组 Group_u 的目标节点，直接利用对抗性学习将它们与源域对齐可能会导致负迁移，因为 Group_u 可能包含来自已知和未知类的目标节点。暴力地强制目标未知类节点与源节点对齐将会破坏学习到的域不变嵌入。为了应对这一挑战，受到 DANCE 的启发，可以利用邻居中心聚类（NCC）来更好地识别已知类和未知类中的目标节点，同时将目标节点与源节点软对齐。NCC 的主要思想是将 Group_u 中的每个目标节点移动到源类中心或 Group_u 中的聚类中心。目标未知类节点更有可能与接近真实未知类中心的中心共享相似的语义信息。同样，来自已知类别的那些可能与已知类别中心具有相似的特征。给定不确定组 Group_u，使用K-means将它们分为K个簇并获得相应的嵌入中心 \{\mu _{t}^{1},...,\mu _{t}^{K}\}。同时，利用权重向量 \mathbf{W}_f=[w_{f}^{1},...,w_{f}^{|C_s|}] 在分类器 中作为源类中心。设 \mathbf{M} 表示由来自 Group_u 的聚类中心和源类中心组成的中心矩阵：
虽然由于阈值 \gamma 的设置，Group_u 同时包含已知类和未知类，Group_u 中的大部分数据属于未知类。因此，\mathbf{M} 主要用于对未知类数据进行聚类；同时，为了避免已知类数据出现负聚类，在 \mathbf{M} 中添加源类中心。为了更好地区分已知和未知数据，我们提出等式：
其中 \left< \cdot ,\cdot \right> 表示两个向量之间的内积来衡量它们的相似度，\tau 表示温度参数，根据经验设置为0.05。最终，邻居中心聚类损失被表述为：
其中 N_{group_u} 是不确定组 Group_u 中目标节点的数量。通过最小化上述损失，学习到的目标嵌入空间将更具辨别力。
总损失目标包括三个组成部分。交叉熵损 \mathcal{L} _{ce} 适用于源图上。等式中的对抗域对齐损失 \mathcal{L} _{adv} 和邻居中心聚类损失 \mathcal{L} _{ncc} 用于源图和目标图。因此，总体损失函数为：
其中 \alpha 是控制邻居中心聚类强度的超参数。
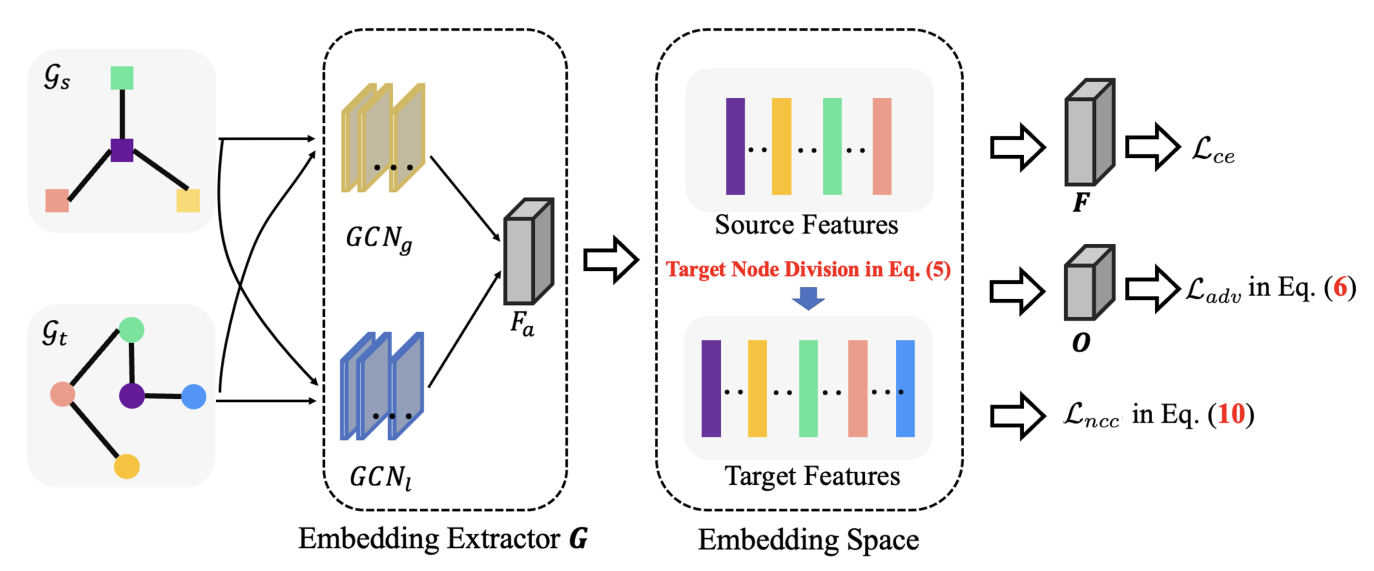
用于开放集图域自适应的新颖的分离域对齐（SDA）方案，其中包括三个损失：交叉熵损失、域对齐损失和邻居中心聚类损失以及三个模块：特征提取器 G = \{GCN_g, GCN_l, F_a\}，分类器 F 和域鉴别器 O。
局部 GCN (GCNl) 为了捕获图中的局部信息，直接利用（Kipf 和 Welling 2017）提出的 GCN 模型，并将局部 GCN GCNl 表示为一种前馈神经网络。给定图 G = (V, E, A, X, Y )，GCNl 的第 i 个隐藏层 Z(i) l 的输出定义为：
全局 GCN (GCNg) 为了挖掘全局拓扑特征，我们引入了基于 PPMI 的 GCN（Zhuang and Ma 2018），利用 PPMI 矩阵 P 来评估给定图 G 内节点之间的拓扑邻近度（k 步骤）。有关 P 的更多详细信息，请参阅（Zhang and Ma 2018）。
Embedding Attention (Fa) 为了进一步挖掘局部嵌入Zl和全局嵌入Zg这两种嵌入的贡献，并生成统一的节点嵌入空间，引入了注意力层Fa。 α1 和 α2 来自自注意力层 Fa，输入为串联的 Zl 和 Zg。 Fa 以 Zl 和 Zg 作为输入，分别生成 Zl 和 Zg 的权重系数 α1 和 α2：