原文：Beyond the Known: Novel Class Discovery for Open-World Graph Learning | SpringerLink

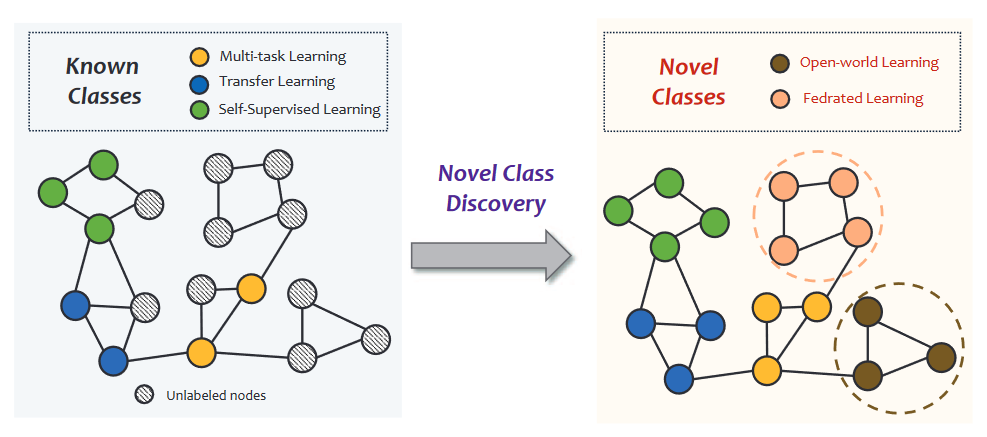例子：在学术图上展示开放世界学习的新颖类发现的插图。节点代表论文，边代表引用关系，每篇论文属于某个研究领域（节点类）。

• 构成了研究开放世界图神经网络的首次尝试，该网络可以自动发现图上的新类。

• 提出了原型注意力网络（prototypical attention network）来检测和消除类间相关性，以便在表示学习期间将新类与其他类区分开来。

• 为了缓解新颖类标签信息的缺乏，根据多尺度图特征和从已知类中挖掘的标签粒度生成伪标签。

问题设置

图表示为 G = (\mathcal{V, E, X})，其中 \mathcal{V} 表示图中节点的节点集，\mathcal{E} 是表示边集，\mathcal{X} 表示节点的特征集。

开放世界图学习中节点集V由标记的训练节点 \mathcal{V}_L 和未标记的测试节点 \mathcal{V}_U 组成，它们分别属于类集 \mathcal{Y}^L 和 \mathcal{Y}^U。在开放世界场景中，新的类可以出现在未标记的节点上，即 \mathcal{Y}^L \sub \mathcal{Y}^U。开放世界图学习的目的是自动发现新类，并将未标记的节点分类为已知类（\mathcal{Y}^L）或新类（\mathcal{Y}^U\backslash\mathcal{Y}^L）。

方法

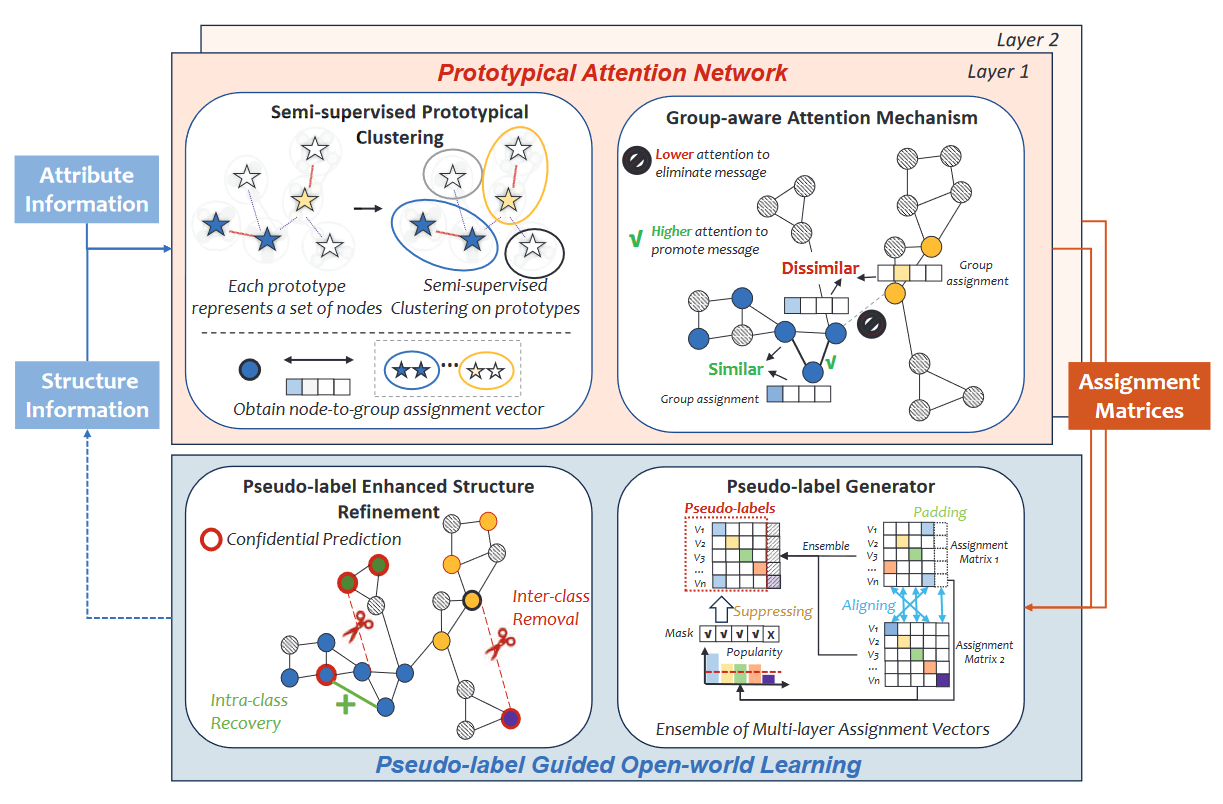提出的 ORAL 方法的框架如图所示。首先采用原型注意力网络（PAN）来消除类间相关性。给定原型学习提取的代表节点（原型），PAN对规模相对较小的原型图进行半监督聚类，有效地获得原型和节点的分组分配。群体感知注意力机制消除了群体之间的消息传递，以生成可分离的表示。此外，ORAL 缓解了伪标签生成器缺乏标签信息的问题，伪标签生成器在最后阶段对齐和集成多个组分配估计，通过结构细化促进开放世界学习。

原型注意力网络（PAN）

原型注意力网络将节点聚类成组，并通过减少组之间的消息传递来消除类之间的相关性，其中聚类结果是真实标签的近似值。尽管如此，开放世界中新类的数量是未知的，我们必须在图上重复执行聚类，通过拟合标签信息来搜索最佳聚类粒度，这可能非常耗时。为了减轻计算负担，我们通过原型学习提取代表节点，并在小原型图上进行半监督聚类，而不是整张图。节点聚类结果近似于原型的结果，用于消除通过群知注意机制传递的消息。

代表节点被建模为表示空间中的一组可训练原型 \mathcal{C}=\{\mathbf{c}_1,\mathbf{c}_2,\cdots\mathbf{c}_{N_{pro}}\}，其中 N_{pro} 表示原型的数量。给定一个具有表示 \mathbf{h}_i 的节点，该节点对应初始化为节点特征 \mathbf{x}_i，我们计算每个原型 \mathbf{c}_j 对于该节点的代表性得分如下：

为了确保每个原型都代表一组节点，我们将代表性分数的边缘分布规范化为接近平均分布，

其中 \mathbf{r}_i = \left[r_{i1},\ldots,r_{iN_{nro}}\right]\in\mathbb{R}^{N_{pro}}, \mathbf{1}\in\mathbb{R}^{N_{pro}} 表示全 1 向量，KL 表示 Kullback-Leibler 散度。每个节点被视与具有前 k 个最大代表性得分的原型的相关联。原型 \mathbf{s}\in{\mathbb{R}^{N_{pro}\times N_{pro}}} 之间的相似关系可以计算为其关联节点集的杰卡德指数，即 \begin{aligned}s_{ij}=\text{Jaccard}(\Gamma_i,\Gamma_j)\end{aligned}，其中 \Gamma_i 表示第 i 个原型的关联节点集。

给定两个集合A,B，Jaccard 系数定义为A与B交集的大小与A与B并集的大小的比值，定义如下：

J\left(A,B\right)=\frac{\left|A\cap B\right|}{\left|A\cup B\right|}=\frac{\left|A\cap B\right|}{\left|A\right|+\left|B\right|-\left|A\cap B\right|}

asd