原文:
问题设置
Few-shot 学习任务的数据可以分为三部分:训练集 Dtrain、支持集 Dsupport 和测试集 Dtest。具体来说,Dtrain 有大规模的训练样本(例如,一个类别大约有数百个样本),这些样本的类别记为 Cbase。它提供了大量的先验知识作为已知内容来帮助描述其他样本。支持集 Dsupport 和测试集 Dtest 有相同的类别,称为 Cnovel,与训练集 Cbase 中的类别不相交。 Few-shot Learning 的目标是利用训练集和支持集学习一个图像分类模型,该模型能够准确地将测试集中的图像从新类别中分类,其中新类别的训练样本采样自Dsupport 而测试中的样本属于 Dtest。它通常关注 N-ways-K-shots 识别问题,识别 N 个新类别,每个类别有 K 个支持样本。
方法
特征混合
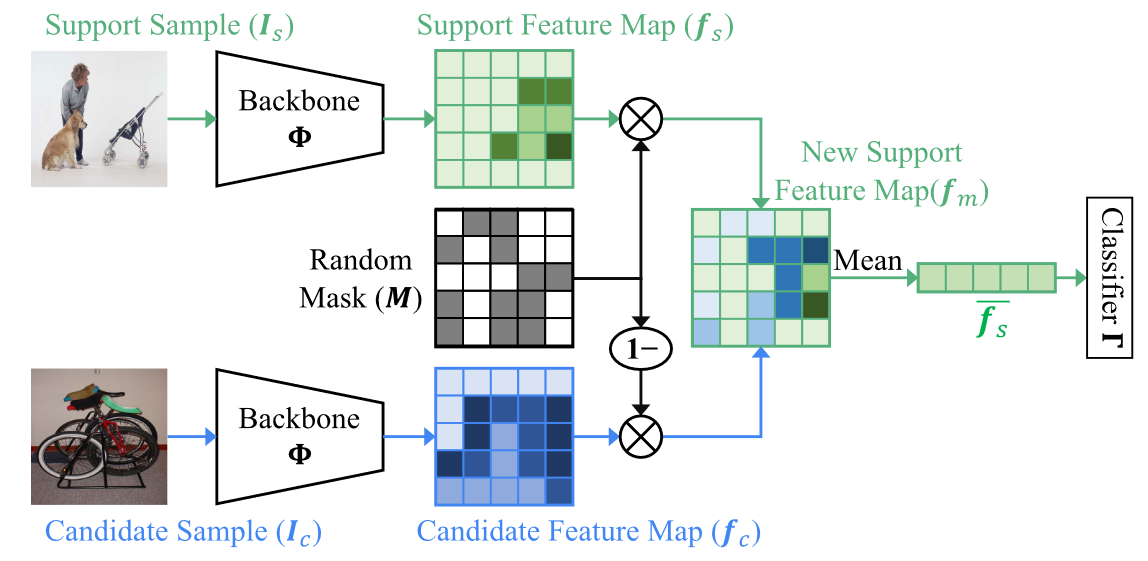
为了保留输入图像(用于 FSL 任务)的更多信息,我们在特征混合操作之前通过预训练的视觉 CNN \Phi 将图像表示到特征图中,其中 \Phi 已经在此类已知图像上进行了训练(训练集 Dtrain 在 Cbase 类别中)。具体来说,给定图像作为输入,我们从 CNN 的最后一个卷积层中提取计算结果(特征图)。将 CNN 的输入图像表示为 \boldsymbol{I},特征图 \boldsymbol{f}\in\mathbb{R}^{W\times H\times C} 可以表示为 \Phi(\boldsymbol{I}),其中 W 、 H 和 C 分别是宽度、高度和分别是通道维度。然后,说明我们的特征混合(feature mixture)操作。在此操作中,用于混合的两个特征图属于不同的集合。通常,一个特征图来自支持集,另一个特征图来自训练或测试集(称为候选集)。我们将这两个集合分别定义为 \mathcal{F}_{s}=\{\boldsymbol{f}_{s}^{i}\}_{i=1}^{N\times K}, \mathcal{F}_{c}=\{\boldsymbol{f}_{c}^{i}\}_{i=1}^{L},其中 L 是候选集的特征数量。将支持集和候选集的特征图分别表示为 \boldsymbol{f}_{s} 和 \boldsymbol{f}_{c},我们首先随机屏蔽支持特征 \boldsymbol{f}_{s} 中的部分值,然后用候选特征 \boldsymbol{f}_{c} 相同位置的值填充屏蔽值。具体来说,我们定义一个与特征图 \boldsymbol{f}大小相同的均匀分布随机矩阵 \bar{\boldsymbol{M}}\in(0,1),然后使用超参数 α 来控制变换后的掩码矩阵 \boldsymbol{M} 对 \boldsymbol{f}_{s} 和 \boldsymbol{f}_{c} 之间的混合比例,其中掩码矩阵 \boldsymbol{M} 由随机矩阵 \bar{\boldsymbol{M}} 计算得出:
在此操作中,较大的 α 将引入更多来自其他特征图的干扰,并且混合特征图更具判别力。同时,为了通过控制生成特征的分布来提高模型的泛化性和鲁棒性,我们还遵循 MixUp 和 CutMix 引入了组合比 λ\sim\mathrm{Beta}(2, 2)。因此,我们的混合的混合特征图 \boldsymbol{f}_m\in\mathbb{R}^{W\times H\times C} 可以计算为:
在我们的少样本分类器学习中,混合特征图 \boldsymbol{f}_{m} 和支持特征图 \boldsymbol{f}_{s} 都被添加到训练集中。与按比例混合真实标签的 MixUp 和 CutMix 不同,我们保持两者标签相同,以避免在分类器训练阶段引入噪声监督。
相似性约束

在传统的基于混合的方法中,候选集 Fc 通常由训练集(Dtrain)的全部特征组成。然而,大量的训练样本增加了混合运算的计算成本,降低了训练效率。这是因为从 Dtrain 中随机选择的特征会减慢分类器的优化速度。为了解决这个问题,我们通过设计相似性约束来过滤候选样本并构造新样本。具体来说,给定支持集的特征图 f s 及其候选集 Fc = { f i c}L i=1,我们首先通过平均池化操作将这些特征图转换为特征,即 ̄f s 和 ̄ Fc = { ̄f i c}L i= 1.然后我们计算这些特征之间的相似度 S = {si }L i =1
其中⟨•,•⟩是两个向量之间的内积。最后,我们对相似度分数S进行排序,并通过删除远离支持特征 ̄f s的特征图来简化候选集。图中描绘了一个示例,给定“Retriever”样本,我们展示了它与特征空间中其他样本之间的相似性。然后,我们选择相似的特征,即“Chime”和 “Gordon Setter”,作为“Retriever”的候选特征。尽管“Chime”和“Retriever”在任何属性上都不相关,但由于预训练的 CNN 可能引入的偏差,它们彼此相似。因此,使用“Retriever”和“Chime”构建新样本可以帮助分类器关注支持样本的特征分布。
在我们的实验中,我们发现设置相似度阈值来控制过滤操作并不容易。这是因为极限支持特征的相似度集 S 都小于某个阈值。因此,我们选择相似度集中得分最高的Q个样本来构成新的候选集。
训练和推理
对于训练,我们使用可用的预训练主干来提取样本(基础类和新类)的特征图。然后,我们使用这些特征图通过特征混合操作来训练分类器。最后,我们使用经过训练的分类器来识别新样本。我们方法的分类器只有一个具有归一化权重的全连接层。它将平均池特征分为 N 个新类别。给定批次中的 B 支持特征 { ̄f i s}B i=1 及其混合特征 { ̄f i m}B i=1 ,我们计算分类器的预测与其硬标签 {li }B i=1 之间的损失 L ,然后使用这些损失来优化分类器 0 的参数:
其中 \mathcal{L}_{\mathrm{CE}} 是交叉熵损失函数。 λ 是遵循 MixUp 和 CutMix 设置的权重因子。

为了进行推理,我们使用经过训练的分类器将新样本的平均池特征直接预测到特定类别,其中平均池特征是从预训练 CNN 的倒数第二层中提取的。

