一种图节点级任务 OOD 泛化方法，理论分析部分比较充分。
基本理论
图 OOD 泛化
给定训练集 G_\mathrm{train} = (G_i, Y_i )^{N_i} _{i=1}，其中包含从训练分布 P_\mathrm{train} (G, Y ) 中抽取的 N 个实例。在监督设置中，它的目标是学习一个最佳的图预测器 f^* ，它可以对从测试分布采样的数据表现出最佳的泛化性能：
其中 P_\mathrm{test} (G, Y ) ≠ P_\mathrm{train} (G, Y ) 表示训练集和测试集之间存在分布偏移，在训练集上训练的最优预测器可能无法在测试集上很好地泛化。
图对比学习（GCL）
图对比学习是一种具有代表性的自监督图学习方法。给定输入图 G，使用两个图增强 τ_α 和 τ_β 分别生成两个增强视图 G_α = τ_α (G) 和 G_β = τ_β (G)。然后将 GNN 模型 g_θ 应用于增强视图以生成节点表示 g_θ (G_α )∈\mathbb{R}^{ N ×D}。最后，将对比损失函数应用于表示，将正对拉在一起，同时将负对推开。以InfoNCE损失为例，公式如下：
其中 G' 表示从图数据分布 \mathcal{G} 中随机采样的图，作为非坍塌的约束。为简单起见，编码器生成的表示自动标准化为单位球体，即 ∥g_θ (G) ∥ = 1, ∀G ∈ \mathcal{G}。通过最小化这种损失，前一项（又名对齐损失 \mathcal{L}_\mathrm{align}）通过鼓励正对的相似性将正对拉到一起，后一项（又名均匀性损失 \mathcal{L}_\mathrm{uniform}）将负对分开。然后通过最终表示的线性可分离性来评估预训练图编码器的质量。也就是说，线性分类器 p_ω 建立在冻结编码器之上：
其中 g^∗_θ (\cdot) 是通过最小化不带标签的式(1)获得的。为了评估预训练模型，最佳图预测器 f^∗_φ = p^∗_ω\circ g^∗_θ 将应用于测试数据。
GCL-OOD：面向 OOD 泛化的图对比学习
假设 Φ(G) 是输入实例 G 的不变原理，它在遵循不变性假设的不同环境（增强）中是稳定的：
其中 \mathcal{E}_\mathrm{tr} 表示训练环境集（不同环境下的数据有不同的分布），上式表示不变原理与不同环境中的语义标签表现出预测不变（稳定）相关性。最优（不变）图编码器 g_\theta^{\star} 在所有环境中实现不变原理 Φ(G)（假设增强函数不会改变原始输入的语义标签）：
然而，在 GCL 的预训练过程中，我们无法在自监督环境下访问标签。在这里，我们参考先前的工作，在前述的损失 \mathcal{L}_{\mathrm{MI}}\left(g_\theta ; \mathcal{G}, \pi\right) 和下游损失 \mathcal{R}(g_θ ;\mathcal{G}^{\mathrm{tar}}) 的上界之间建立联系：
其中 c 是一个正常数，\zeta (σ,δ) 是一组仅依赖于 (σ, δ) 增强的常数，C_k ⊆ \mathcal{G} 是 k 类中数据点的集合，\mu_k(g_\theta;G):=\mathbb{E}_{G\thicksim\mathcal{G}}[g_\theta(G)],k ∈ [K]，具体的推导这里不做展开，这里只是为了证明通过 GCL 实现 OOD泛化的理论可行性，详细参考原文 Appendix。
式(2)中的第一项是在 \mathcal{G} 上预训练期间优化的对齐损失。第二项由数据增强的 (σ, δ) 数量决定，较大的 σ 和较小的 δ 导致较小的 \zeta (σ,δ)。第三项与线性层 p 相关，并在下游训练中最小化。可以通过选择适当的正则化项 \mathcal{L}_\mathrm{uniform} 来区分类中心，从而导致第三项通过 p_ω 变为 0。简而言之，式(2)意味着在具有增强函数 τ 的分布 \mathcal{G} 上的对比学习本质上优化了增强分布 \mathcal{G}_\tau 上的监督风险上限，从而导致较低的监督风险。因此，即使没有标签，我们也可以通过修改当前 GCL 方法中的主要组成部分，在一定程度上实现预训练期间的最优（不变）图编码器。
偏移鲁棒图对比学习
在上述理论基础下，本节介绍作者的与模型无关的方法，用于改进 GCL 方法的 OOD 泛化，称为 MARIO（Model-Agnostic Recipe for Improving OOD generalization of GCL methods）。
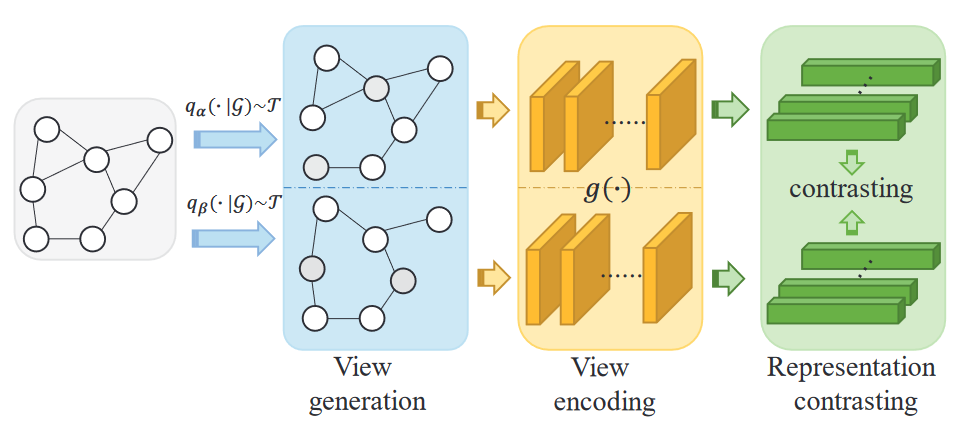图对比学习流程如图，MARIO 方法主要应用于视图生成（蓝）和表示对比（绿）两个阶段，这也意味着可以在视图编码（黄）部分采用不同的网络结构。
图增强（视图生成）的分析与改进
定义 1（不变风险最小化，IRM）。如果存在一个对 \mathcal{B} 中的所有域同时最优的分类器 p_{\omega^*}，我们称数据表示 g_θ 会在域集 \mathcal{B} 上引发不变预测变量 p_\omega\circ g_\theta：
其中 \mathcal{R} 是在域 \mathcal{G} 上测量的预测变量 p_\omega\circ g_\theta 的风险。
经验和理论都证明，这些引发不变预测变量的特征（表示）g_θ 可以增强监督学习中跨分布变化的模型的泛化能力。通过将 \mathcal{B} 设置为增强图集 \{\mathcal{G}_\tau\}_{\tau\in\mathcal{T}}，这个概念可以很容易地应用于与之前的工作进行图对比的学习方法。以下不变对齐损失的定义是 GCL-OOD 问题的建议损失函数。
定义 2（不变对齐损失）。编码器 g_θ 在分布 \mathcal{G} 上的不变对齐损失 \mathcal{L}_{\mathrm{align}^*} 定义为
不变对齐损失衡量的是在最具“挑战性”的两次增强下两个表示之间的差异（即取表示差异上界求期望），而不是式(2)中的微不足道的期望。直观上，它避免了编码器在不同 \mathcal{G}_\tau 中表现极其不同的情况。
理论 1（不同领域的变异上限）。对于两个增强函数 τ 和 τ'、线性预测器 p 和表示 g，不同域之间的变化上限为
进一步固定 g 并令 p_\tau\in\arg\min_p\mathcal{R}\left(p\circ g,\mathcal{G}_\tau\right)，有
Proof:
(4)\Rightarrow(5)即使用经验损失的定义；(5)\Rightarrow(6)展开消去 Y^2 并整理；(6)\Rightarrow(7)取 c 大于等于(6)中第二项即可；(7)\Rightarrow(8)提出p；(8)\Rightarrow(9)定义2。
\mathcal{L}_{\mathrm{align}^*} 的定义(3)将式(1)中在 \mathcal{T} 上的求的期望替换为 \mathcal{L}_{\mathrm{align}} 的上界，导致 \mathcal{L}_{\mathrm{align}}(g;\mathcal{G},\pi)\le\mathcal{L}_{\mathrm{align}^*}(g,\mathcal{G}),\forall g,\pi，增强函数 τ 是根据分布 π 从增强池 \mathcal{T} 中随机选择的。根据理论1当 \mathcal{L}_{\mathrm{align}^*} 优化为较小值时，表明 \mathcal{R}\left(p\circ g;G_\tau\right) 在不同的增强函数 τ 中保持一致，这意味着 \mathcal{G}_\tau 的最佳表示与 \mathcal{G}_{\tau'} 类似。也就是说，较小的 \mathcal{L}_{\mathrm{align}^*} 表示往往会在不同的域中引发相同的线性最优预测器，这是原始对齐损失中缺乏的属性。
用 \mathcal{L}_{\mathrm{align}^*} 代替 \mathcal{L}_{\mathrm{align}} 的一个问题是难以估计 \sup_{\tau,\tau^{\prime}\in\mathcal{T}}\|g(\tau(G))-g\left(\tau^{\prime}(G)\right)\|^2，因为它需要迭代所有增强方法。为了有效地找到连续空间中的最坏情况，我们转向对抗训练来近似supermum算子：
其中内循环最大化损失以逼近最具挑战性的扰动，其强度 \|\delta\|_p\leq\epsilon 被严格控制，以便它不会改变原始视图的语义标签，例如 \epsilon=1e-3。考虑到训练效率，在本文中，我们遵循并进一步修改有监督图对抗训练框架 FLAG，以适应无监督图对比学习，如下所示：
表示对比的分析与改进
式(1)这样的普通对比损失旨在最大化正对之间互信息的下限。然而，存在一些冗余信息（即条件互信息）可能会阻碍图对比学习的泛化。我们的目标是学习与下游任务相关的最小充分表示，这可以有效减轻过度拟合并展示对分布变化的鲁棒性，提高 GCL 方法的泛化能力。
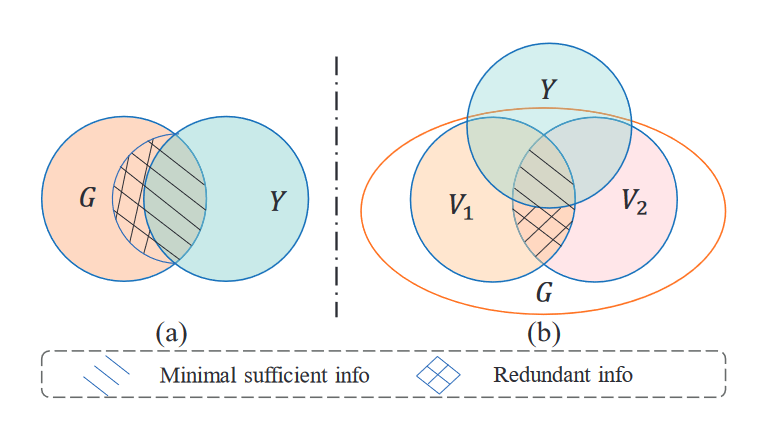受信息瓶颈原理（IB）的启发，IB 原则旨在学习给定任务的最小充分表示。它通过最大化表示和目标之间的互信息（充分性）同时限制表示和输入数据之间的互信息（最小值）来实现这一点，如图所示。修改对比损失来摆脱监督信号以及学习广义表示：
定义 3（信息瓶颈，IB）。令 X, Z,Y 分别表示输入、嵌入和标签的随机变量。信息瓶颈训练目标的表述为
其中 I_θ 表示互信息估计器，参数为 θ，且 β > 0 控制压缩和下游任务性能之间的权衡（较大的 β 导致较低的压缩率，但嵌入 Z 和标签 Y 之间的 MI 较高）。
受这一原理的启发，我们将普通对比损失[63,67,68]修改为等式19。当前的图对比学习方法旨在最大化正对之间的互信息，如图2b所示。然而，在具有可用训练标签的场景中，普通对比损失中的一些信息变得多余。在图2b中，V 1 和V 2 表示来自同一样本G的两个增强视图，U和V表示它们各自的表示。消除这些冗余信息符合 IB 原则。为了更准确地描述这种冗余，我们引入了条件互信息（CMI）。
定义 4（条件互信息，CMI）。条件互信息 I (U ;V | Y ) 衡量给定 Y 的情况下 U 和 V 之间 MI 的期望值，可以表示为
为了减少冗余信息，从而提高OOD泛化能力，我们需要最小化两个视图 U 和 V 之间的 CMI 。然而，估计上面的方程是很困难的。所以利用互信息估计器（例如，Donsker-Varadhan 估计器、Jensen-Shannon 估计器、InfoNCE）来估计条件互信息。以 InfoNCE 为例，CMI 目标可以近似为：
其中 \mathrm{sim}(x, y) 是余弦相似度函数，正对是从条件联合分布中抽取的，负对是从条件边缘分布的乘积中抽取的。简而言之，我们首先对 y ∼ Y 进行采样，然后从 P_{U ,V |y} 和 P_{U |y} P_{V |y} 中采样正负对。式(1)的负格式是 \mathrm{CMI}\ I (U ; V | Y ) 的下限。
在线聚类
将上述近似应用于我们的无监督预训练的主要挑战是缺乏标签 Y。故利用在线聚类技术来获取伪标签。这些伪标签在训练过程中被迭代地细化，确保它们与真实标签的互信息增加。为了将聚类集成到我们的前置任务中，将为每个簇 i 初始化可学习原型 c_i，矩阵 C = [ c_1 ,c_2 ,\cdots ,c_K ] 收集所有列原型向量。对于聚类，简单地计算节点 i 的 K 个原型与节点表示 u_i 和 v_i 之间的相似度：
其中原型 C 通过解决交换预测问题（即根据另一个视图的表示来预测一个视图的表示）来更新：
聚类损失通过比较聚类分配而不是它们的表示来关注对比节点。然而，这可能会导致一种简单的解决方案，其中所有样本都在一个簇中。为了防止这种情况，我们引入了相等原型分配分区的约束。通过这些原型，我们可以推断节点表示的伪标签：
最终的鲁棒变换对比损失可以表示为
其中 I_\theta(U;V)、I_\theta(U;V\mid\hat{Y}) 可分别实例化为公式(1)和公式(11)；γ ≥ 0 控制压缩和前置文本任务性能之间的权衡，类似于式(10)。直观地，如果正对已经在特征空间中共享相同的语义标签（即属于同一簇），目标将减少他们的共享信息，以避免在训练过程中学习冗余信息和过度拟合，这将为 OOD 泛化带来性能提升。