原文:Learning Invariant Graph Representations for Out-of-Distribution Generalization (neurips.cc)
Graph OOD 常见的 baseline 之一
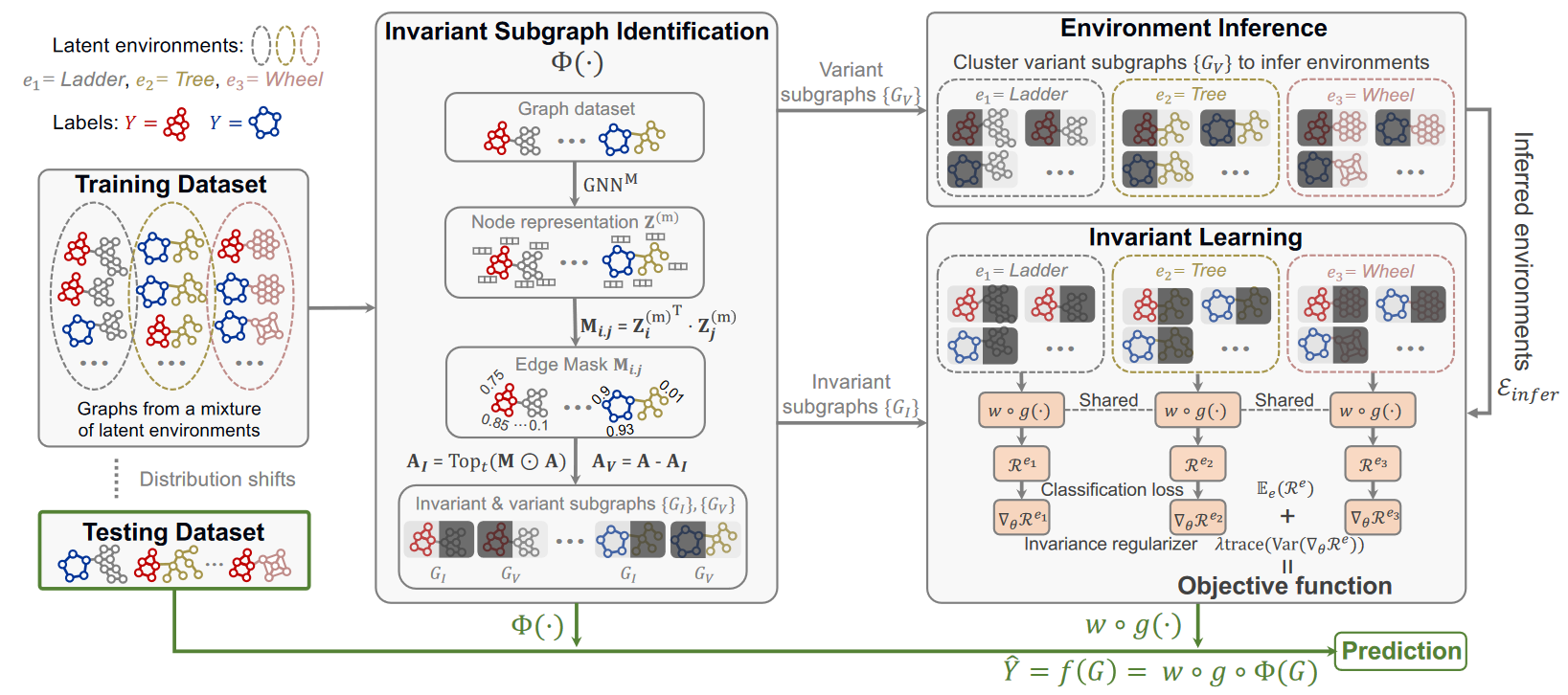 问题设置
问题设置
令 \mathbb{G} 和 \mathbb{Y} 为图和标签空间。我们考虑一个图数据集 \mathcal{G}=\{(G_i,Y_i)\}_{i=1}^N,其中 G_i ∈ \mathbb{G} 且 Y_i ∈ \mathbb{Y}。遵循 OOD 约定,我们假设数据集是从多个训练环境收集的,即 \mathcal{G}=\{\mathcal{G}^e\}_{e\in\mathrm{supp}(\mathcal{E}_{tr})},其中 \mathcal{G}^e=\{(G_i^e,Y_i^e)\}_{i=1}^{N_e} 表示来自环境 e 的数据集,\mathrm{supp}(\mathcal{E}_{tr}) 是环境变量的支持度训练数据。我们用 G 和 Y 表示图和标签的随机变量,用 G^e 和 Y^e 表示指定环境 e 中的随机变量。
令 \mathcal{E} 表示所有可能环境的索引上的随机变量。我们的目标是找到一个在所有环境下都表现良好的最佳预测器 f^∗(\cdot) : G → Y:
其中 \mathcal{R}(f|e)=\mathbb{E}_{\text{G,Y}}^e[\ell(f(\text{G}),\text{Y})] 是预测变量 f 对环境 e 的风险,I(\cdot,\cdot) : \mathbb{Y} × \mathbb{Y} → \mathbb{R} 表示损失函数。我们进一步分解 f (\cdot) = w \circ h,其中 h(\cdot) : \mathbb{G} → \mathbb{R}^d 是表示学习函数,d 是维度,w(\cdot) : \mathbb{R}^d → \mathbb{Y} 是分类器。请注意,\mathrm{supp}(\mathcal{E}_{tr})\subset \mathrm{supp}(\mathcal{E})。此外,分布平移表明 P^e(G, Y) \ne P^{e'}(G, Y),e\in\mathrm{supp}(\mathcal{E}_{tr}),e'\in\mathrm{supp}(\mathcal{E}),即图和相应的标签的联合分布对于训练和测试图数是不同的。
但上面这个目标问题难以直接实现,因为为大多数实际场景收集图环境标签的成本过高,所以图的环境标签 e 实际上是不可观察的。所以需要进行一个问题的转换,首先需要从混合潜在环境中收集但没有环境标签的图数据集 G 推断图环境 \mathcal{E}_{\mathrm{infer}},即 \mathcal{G}=\{\mathcal{G}^e\}_{e\in\mathrm{supp}(\mathcal{E}_{infer})},并学习在推断环境 \mathcal{E}_{\mathrm{infer}} 下取得了良好的OOD泛化性能图预测器 f^*(\cdot)。
方法
不变子图识别
假设每个输入图 G ∈ \mathcal{G} 都有一个不变子图 G_I ∈ \mathcal{G},它与标签的关系在不同环境中是不变的。我们将图的其余部分(即补集)称为变体子图,并将其表示为 G_V,它表示与标签的关系在不同环境中变化的图形部分,例如虚假相关性。因此,如果模型能够识别不变子图并且仅使用来自 G_I 的结构信息,那么该模型将具有更好的 OOD 泛化能力。
将获得不变子图的生成器表示为 G_I = Φ(G)。Φ(G) 需要满足不变性(存在一个子图生成器,它可以在不同环境下生成不变的子图)和充分性(生成的不变子图在预测图标签方面应该具有足够的预测能力)。
要将输入图 G 拆分为 G_I 和 G_V,常见的策略是在邻接矩阵 A 上使用二元掩码矩阵 M = \{0, 1\}^{n×n},然而直接优化离散矩阵很困难,对每个图单独学习掩码矩阵也不利于性能泛化,故采用共享可学习的GNN(记为 \operatorname{GNN}^{\mathbf{M}})来生成软掩模矩阵:
A_I 和 A_V 分别表示 G_I 和 G_V 的邻接矩阵,⊙ 表示逐元素矩阵乘法,\operatorname{Top}_t(\cdot)选择具有最大值的元素的顶部 t 百分比。
环境推断
不变子图捕获了预测图结构信息和标签之间的不变关系,因此变体子图反过来捕获了不同分布下的变体相关性,这是环境判别特征。所以可以使用变体子图来推断潜在环境。我们采用另一个 GNN 编码器,其参数也在不同图之间共享,来生成变体子图 G_V 的表示:
其中 READOUT 是一个排列不变的读出函数,它将节点级表示 Z_V 聚合为图级表示 h_V。所有变体子图的表示表示为 H = [h_{V_1} , ..., h_{V_N} ]。获得 H 后,我们使用现成的聚类算法来推断环境标签。在本文中采用 k-means 作为聚类算法:
不变学习
在获得推断的不变子图和环境标签后,我们提出不变学习模块。目标是通过优化最大不变子图生成器准则来学习最优生成器Φ^*。
相对于 \mathcal{E} 的不变子图生成集\mathcal{I} 定义为:
可以证明,生成器 Φ(G) 是满足假设的最优生成器当且仅当它是最大不变子图生成器,即
此处 I(\cdot,\cdot) 是标签和生成的子图之间的互信息。然而直接求解上式对于非线性 Φ 来说是困难的。所以将方程转化为不变性正则化器:
其中 f (\cdot) = w \circ g \circ \Phi,θ 表示所有可学习的参数。g(\cdot) 是不变子图的表示学习函数,w(\cdot) 是分类器。我们将 g(\cdot) 实例化为另一个 GNN,如下所示:
Z_I 和 h_I 分别是不变子图 G_I 的节点级和图级表示。w(\cdot) 被实例化为多层感知器,后跟 softmax 激活函数。它们共同作为我们的表示学习方法 h(\cdot),即 h = g \circ \Phi。

