Logo

菜单

【技术】GCN原理及Pytorch实现

Dymay
Dymay
发布于 2024-06-24 / 23 阅读
0
0

【技术】GCN原理及Pytorch实现

图神经网络的原理

图结构不同层次的任务：

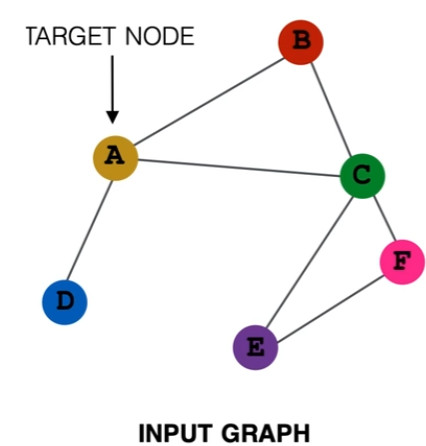
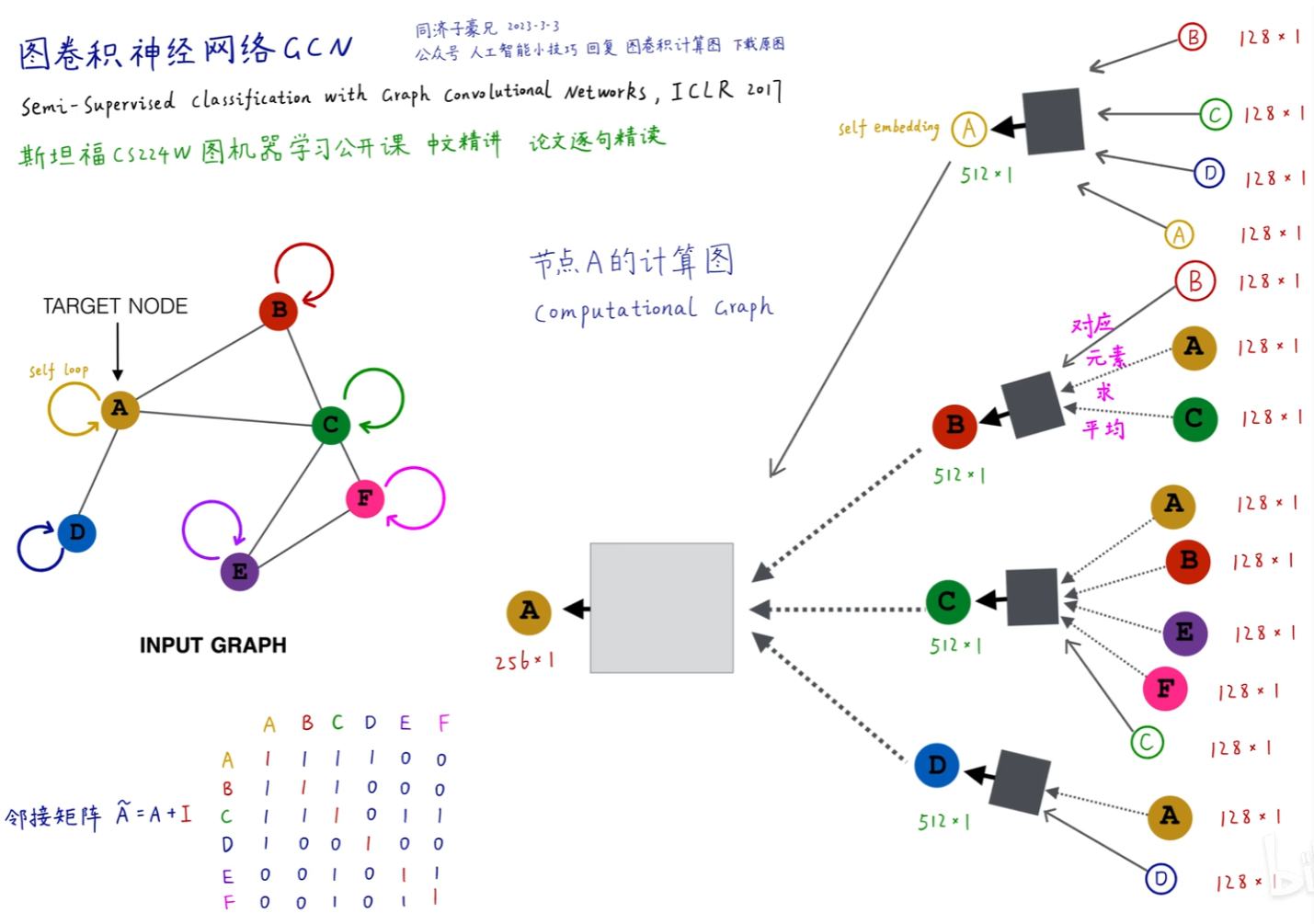
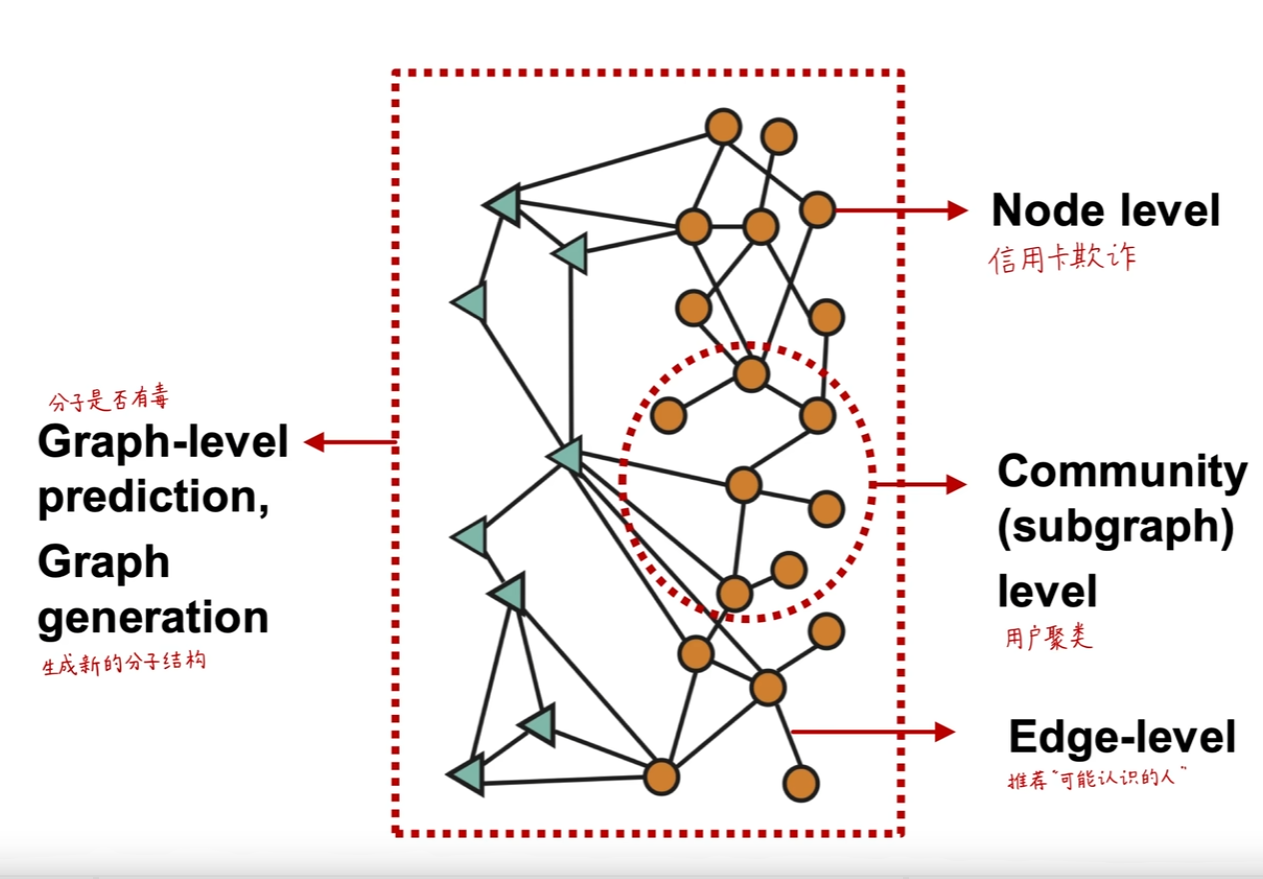图神经网络的基本原理是将图中的节点编码映射为一个低维连续稠密的向量，该向量能反映原节点在图中的连接和属性关系（该过程也称为图嵌入表示学习）。有了节点嵌入，进一步就能得到子图、全图的嵌入向量，最终用于下游任务。要实现这种表示，通常通过消息传递的方法来不断整合邻居节点（或者加上自身）的嵌入来更新自身节点的嵌入，这里通常采用求和、求平均或求最大等方法来整合保证顺序不变性，即相同局部结构习得的表示是一致的，与节点编号无关。可以根据这种过程构建每一个节点的计算图（在训练GCN时的 batch size 就是同时训练的计算图个数，GCN的层数也是指计算图的层数）：

GCN的数学形式

\begin{align} & h_v^{(0)}=x_v\\ & {\color{Blue} h_{v}^{(k+1)} } = {\color{Green} \sigma(}{\color{Red} w^{(k)}}\sum_{u\in N(v)} \frac{{\color{Blue} h_{u}^{k}} }{|N(v)|}{\color{Green} )}\\ & z_v=h_v^K\\ \end{align}

令 \displaystyle H^{(k)}=\left[h_1^{(k)} \ldots h_{|V|}^{(k)}\right]^{\mathrm{T}}，那么\displaystyle\sum\limits_{u \in N_v} h_u^{(k)}=\mathrm{A}_{v,:} \mathrm{H}^{(k)}；考虑度矩阵 \displaystyle D_{v, v}=\operatorname{Deg}(v)=|N(v)|，取逆有 \displaystyle D_{v, v}^{-1}=1 /|N(v)|。则GCN中求均值部分可以写成矩阵形式：

\sum_{u\in N(v)} \frac{{\color{Blue} h_{u}^{k}} }{|N(v)|} \Rightarrow D^{-1}AH^{(k)}


其中 D^{-1}A 为行标准化的邻接矩阵，最大特征值为1。但使用这种行标准化的邻接矩阵只按照自己的度取平均，没有考虑邻居的连接数（重要程度）。一个简单的解决方法是采用简单对称标准化的邻接矩阵D^{-1}AD^{-1}，同时考虑邻居的度，但这个矩阵的特征值在(-1,1)，输入向量左乘该矩阵后，幅值会变小。所以进一步地，通常采用对称标准化的邻接矩阵D^{-\frac{1}{2}}AD^{-\frac{1}{2}}，保持最大特征值为1。所以有：

\sum_{u\in N(v)} \frac{{\color{Blue} h_{u}^{k}} }{|N(v)|} \Rightarrow D^{-\frac{1}{2}}AD^{-\frac{1}{2}}H^{(k)}\\ {\color{Blue} H^{(k+1)} } = {\color{Green} \sigma(} {} \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(k)}{\color{Green}{\color{Red} W^{(k)}} )}

其中\tilde{A}=A+I，允许在更新节点表示时纳入本身的表示。


进一步地，可以对其他邻接节点和自身采用两种不同的权重：

{\color{Blue} h_{v}^{(k+1)} } = {\color{Green} \sigma(} {\color{Red} w^{(k)}} \sum_{u\in N(v)} \frac{{\color{Blue} h_{u}^{k}} }{|N(v)|}+{\color{Purple} b^{(k)}}h_v^{(k)}{\color{Green} )}

注意这里不是残差连接，如果去掉可学习权重b^{(k)}才是一个恒等映射，构成残差连接。上面的过程写成矩阵形式就是：

H^{(k+1)}=\sigma\left(D^{-\frac{1}{2}}AD^{-\frac{1}{2}} H^{(k)} W^{(k)}+H^{(k)} B^{(k)}\right)

GCN的训练

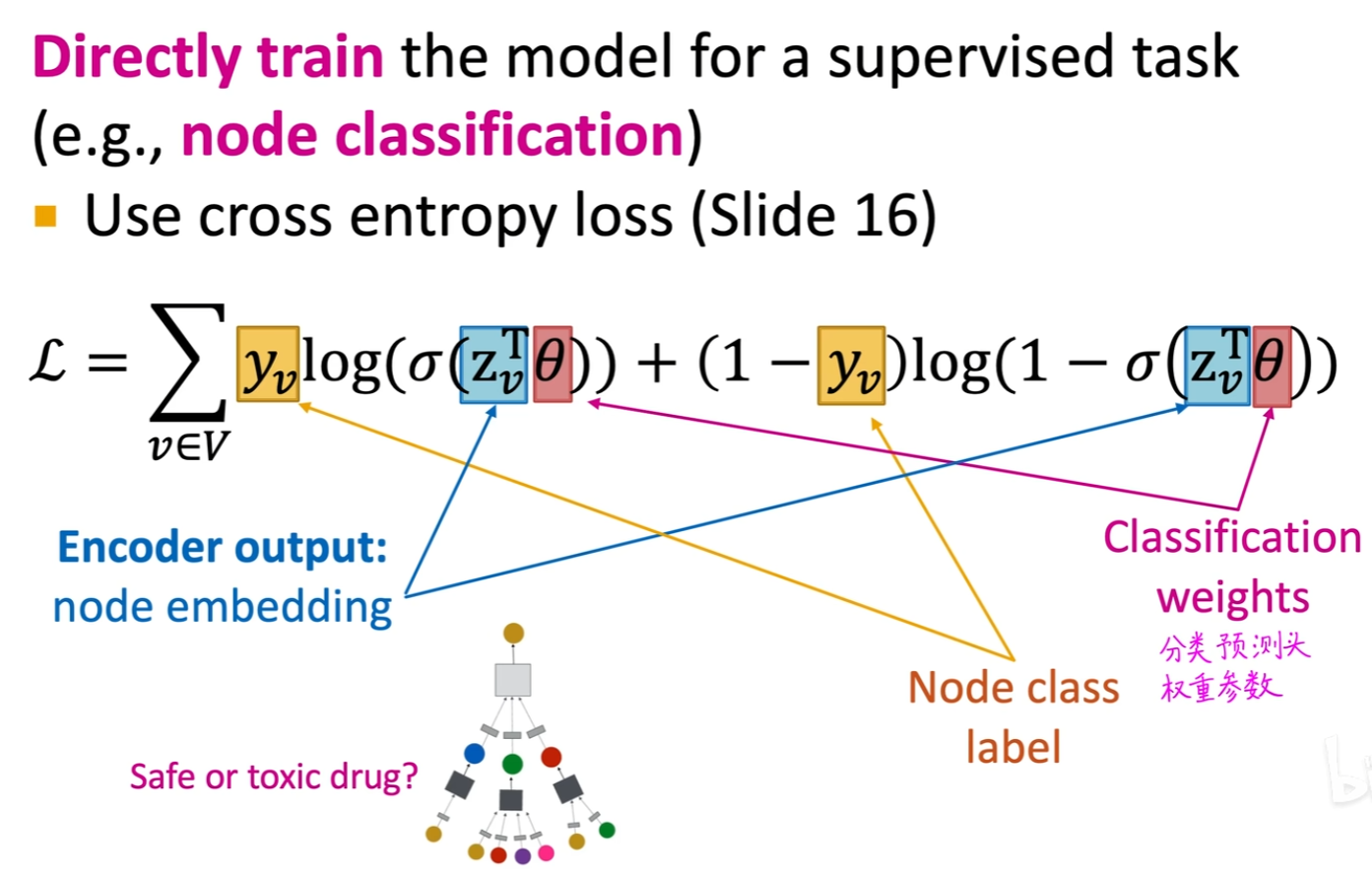
监督学习

如已知一些节点类别，我们就可以加一个分类或回归预测头，对节点得到预测结果，和已知真实类别构建交叉熵损失函数。

无监督学习

直接用图自身结构作为自监督，让原图中结构相近的节点在习得的表示向量空间中的嵌入向量也相近。

GCN的Pytorch实现

PyG（PyTorch Geometric）是基于PyTorch构建的一个库，旨在提供便捷的图神经网络编写和训练工具，用于处理结构化数据的各种应用。它集成了多种用于图形和其他非规则结构的深度学习方法，也被称为几何深度学习。具体的技术文档查阅：PyG Documentation — pytorch_geometric documentation (pytorch-geometric.readthedocs.io)

【论文】开放世界机器学习综述（1）
【论文】理解开放世界半监督学习的图论框架

评论