原文:A Graph-Theoretic Framework for Understanding Open-World Semi-Supervised Learning (neurips.cc)
简介
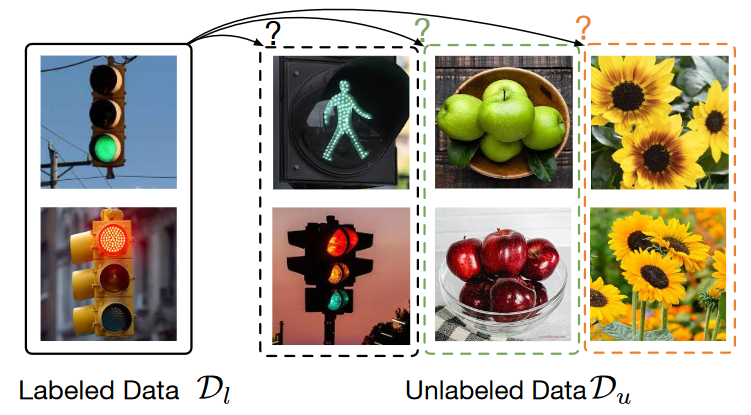
开放世界半监督学习旨在通过利用已知类别的标记集中的先验知识来推断未标记数据中的已知类别和新类别。尽管它很重要,但这个问题缺乏理论基础。本文通过形式化为开放世界环境量身定制的图论框架来弥补这一差距,其中聚类在理论上可以通过图因式分解(Graph Factorizaiton)来表征。我们的图论框架阐明了实用算法并提供了保证。特别是,基于我们的图公式,我们应用了称为谱开放世界表示学习(SORL)的算法,并表明最小化损失相当于在图上执行谱分解。这种等价性使我们能够得出已知类和新类的聚类性能的可证明误差范围,并在标记数据有帮助时进行严格分析。
文章的论述围绕着一个悬而未决的问题:标记数据在塑造已知类别和新类别的表示方面发挥什么作用?
我们形式化了一个为开放世界设置量身定制的图论框架,其中顶点是所有数据点,连接的子图形成类(已知的或新颖的)。边由监督信号和自监督信号的组合定义,反映了标记数据和未标记数据的可用性。重要的是,该图有助于从谱分析的角度理解开放世界的半监督学习,其中聚类在理论上可以通过图分解来表征。基于图论公式,我们通过对比添加标签信息之前和之后所有类的聚类性能来得出形式误差界。在 K 均值测量下,如果一类中的未标记样本与标记数据的总体联系强于其自聚类能力,则它们可以更好地聚类。
问题设置
将经验训练集\mathcal{D}_l\cup \mathcal{D}_u视为标记数据和未标记数据的并集。已标注集\mathcal{D}_l=\left\{ \bar{x}_i,y_i \right\} _{i=1}^{n},无标签集\mathcal{D}_u=\left\{ \bar{x}_i \right\} _{i=1}^{m},其中每个样本\bar{x}_i可以来自已知类别或新类别。设置中无法获\mathcal{D}_u中的标签。为了数学上的方便,将底层标签集表示为\mathcal{Y}_{all},其中\mathcal{Y}_l\subset \mathcal{Y}_{\text{all}}。用表示类的总数C=|\mathcal{Y}_{\text{all}}|。
这种半监督的数据设置对现实世界的应用具有实用价值。标注集在监督学习中很常见,而非标注集可以从模型的运行环境或互联网上自由收集。我们用\mathcal{P}_l和\mathcal{P}分别表示输入空间中标签数据和所有数据的边际分布。此外,我们用\mathcal{P}_{l_i}表示类标签i\in \mathcal{Y}_l 的标注样本的分布。
图论形式
首先正式定义增强图和邻接矩阵。使用\bar{x}表示自然样本(未经增强的原始输入)。给定一个\bar{x},我们使用\mathcal{T} (x|\bar{x}) 来表示x从\bar{x}增广的概率。例如,当\bar{x}表示图像时, \mathcal{T} (\cdot|\bar{x}) 可以是常见增强的分布,例如高斯模糊、颜色失真和随机裁剪。增强使我们能够定义一个通用群体空间\mathcal{X},其中包含所有原始图像及其增强。在我们的例子中,\mathcal{X}由来自标记和未标记数据的增强样本组成,基数\left|\mathcal{X}\right|=N。我们进一步将\mathcal{X}_l表示为来自标记数据部分的样本集(以及增强)
我们用顶点集\mathcal{X}和边权重w定义图G(\mathcal{X},w)。为了定义边权重w,我们将图的连通性分解为两个部分:
通过将\mathcal{X}中的所有点视为完全未标记的自监督连通性w^{(u)}
通过从\mathcal{P}_l向图中添加标记信息的监督连通性w^{(l)}
x和x^+由同一图像\bar{x} ∼ \mathcal{P} 增强,则两个样本 (x, x^+)被视为正对。对于任意两个增强数据 x,x' ∈ \mathcal{X},w^{(u)}_{xx'} 表示生成该对的边际概率,这可以被视为自监督的连接:
半监督场景下可以访问节点子集的标记信息,这允许向图添加额外的连接。x和x^+由具有相同已知类别i的两个标记样本\bar{x}_l和\bar{x}'_l增强,则两个样本 (x, x^+)也被视为正对。换句话说\bar{x}_l和\bar{x}'_l都是独立从\mathcal{P}_{l_i}抽取的。w^{(l)}_{xx'} 表示生成该对的边际概率,这可以被视为有监督的连接:
同时考虑自监督无标签情况 (u) 和引入监督的有标签情况 (l),任何数据对 (x, x')的总体边权重由下式给出:
其中η_u, η_l 调节两种情况之间的重要性。w_{xx'}的大小表示x和x'之间的“正性”或相似性。然后,我们使用 w_x = \sum_{x'\in\mathcal{X}} w_{xx'} 来表示连接到顶点x的总边权重。
通过图的连通性,我们现在可以定义邻接矩阵A ∈ \mathbb{R}^{N×N},其中A_{xx'}= w_{xx'} 。重要的是,邻接矩阵可以分解为两部分:
它可以被视为受到 A^{(l)} 中编码的附加标签信息扰动的自监督邻接矩阵 A^{(u)} 。作为图论中的标准技术,我们使用G(\mathcal{X},w)的归一化邻接矩阵:
其中D ∈ \mathbb{R}^{N×N}是对角矩阵,其中D_{xx}=w_x。归一化平衡了每个节点的度数,减少了度数很大的顶点的影响。归一化邻接矩阵从增强的角度定义了x和x^+被视为正对的概率,这有助于导出学习损失。(归一化矩阵的推导参考【技术】GCN原理及Pytorch实现 - Dymay)
SORL:谱开放世界表示学习
作者提出了一种称为谱开放世界表示学习(SORL)的算法,该算法可以从\tilde{A}的谱分解中推导出来。更重要的是,它允许将学习到的表示和\tilde{A}的前k个奇异向量之间等价起来。这种等价性有助于理论上理解\tilde{A}中编码的聚类结构。具体来说,我们考虑低秩矩阵近似:
根据 Eckart–Young–Mirsky 定理,该损失函数的最小值为F_k ∈ \mathbb{R}^{N×k},使得F_kF^⊤_k 包含\tilde{A}的SVD分解的前k个分量。如果我们将F的每一行 \bold{f}^⊤_x 视为习得的特征嵌入f : \mathcal{X}\to \mathbb{R}^k的缩放版本,则\mathcal{L}_{\mathrm{mf}}(F,A)可以写为对比学习目标的一种形式。
我们为某个函数f定义 \bold{f}_x =\sqrt{w_x}f(x)。中η_u, η_l 是此前定义的系数。那么最小化损失函数\mathcal{L}_{\mathrm{mf}}(F,A)相当于最小化f的以下损失函数,我们将其称为谱开放世界表示学习 (SORL):
其中
在高层次上,\mathcal{L}_1和\mathcal{L}_2将正对的嵌入推得更近,而\mathcal{L}_3、\mathcal{L}_4和\mathcal{L}_5则拉开了负对的嵌入。
\mathcal{L}_1从具有相同类标签的标记数据中采样两个图像的两个随机增强视图
\mathcal{L}_2从\mathcal{X}中的同一图像中采样两个视图
\mathcal{L}_3使用来自\mathcal{X}_l中具有任意两不同类标签的两个样本的两个增强视图
\mathcal{L}_4使用\mathcal{X}_l中的一个样本和\mathcal{X}中的另一个样本的两个视图
\mathcal{L}_5使用\mathcal{X}中两个随机样本的两个视图

