原文：Contrastive Augmented Graph2Graph Memory Interaction for Few Shot Continual Learning

用图结构的对比学习处理 Few-shot 持续学习问题

问题设置

在 FSCIL 任务中，训练集 \mathcal{D}^{(1)},\mathcal{D}^{(2)},\dots,\mathcal{D}^{(T)} 依次到达。每个阶段 \mathcal{D}^{(t)} := \{(x^{(t)}_i , y^{(t)}_i )\}^{|D(t)|}_{i=1} , 1 ≤ t ≤ T ，由输入图像 x ∈ \mathcal{X} 和相应的真实标签 y ∈ \mathcal{Y} 组成。这里，\mathcal{Y}^{(t)} 表示 t-阶段中类别（称为 ways）的标签集，满足 \mathcal{Y}^{(t)}\cap\mathcal{Y}^{(s)}=\empty，其中 ∀s \ne t。第一个阶段 \mathcal{Y}^{(1)} 被称为基础阶段，比后续阶段包含更多的类，并为 \mathcal{Y}^{(1)} 中的每个类提供充足的样本，以促进有效的表示学习以改进分类。后续阶段提供 c 个类（其中 c 远小于 |\mathcal{Y}^{(1)}|）和每类 k 个样本进行训练（称为c-ways k-shot）。对于 2 ≤ t ≤ T 的阶段 t，只有 \mathcal{D}^{(t)} 是可访问的，并且先前阶段的训练集不可用。

基于重放的策略涉及存储一个小型内存缓冲区，其中包含来自先前重放阶段的样本。在后续阶段训练期间添加此缓冲区，以帮助模型回忆先前阶段中的知识。每个阶段的测试集 \mathcal{W}^{(t)} 包括来自当前阶段中所包括的类的样本。在阶段 t 训练后，模型在评估集 \mathcal{E}^{(t)} = ∪^t_{k=1}\mathcal{W}^{(k)} 上进行评估，该评估集统一了当前阶段和所有先前阶段的测试集。

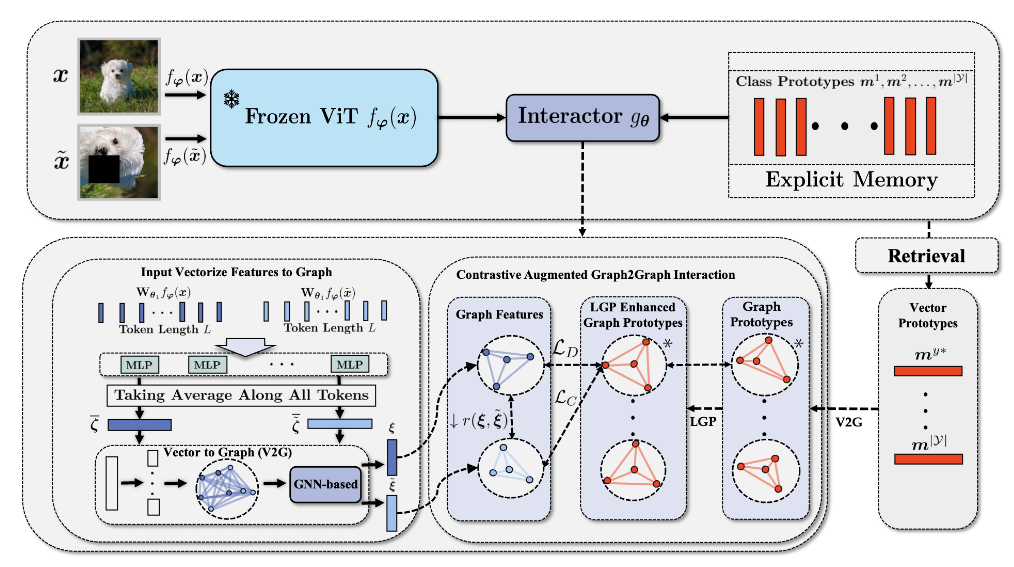方法

整体流程：用预训练好的 ViTf_{\varphi}(\cdot)提取原始样本\boldsymbol{x}和增强样本\tilde{\boldsymbol{x}}的特征，然后分别将这俩特征 \mathbf{W}_{\boldsymbol{\theta}_1}f_\varphi(\boldsymbol{x}),\mathbf{W}_{\boldsymbol{\theta}_1}f_\varphi(\tilde{\boldsymbol{x}}) 进行S等分，每等分的特征再过一个不同参数的 MLP，然后将所有等分的特征过完 MLP 的结求均值得到 \bar{\zeta}，再根据 \bar{\zeta} 建模出图结构。将图过 GNN 之后得到的图表示，再故技重施等分求均值构建图，在输出的原始视图和增强视图的特征之间进行 G2G 对齐。这鼓励提高类内集中度，同时通过 G2G 将两个视图的输出特征与真实标签向量原型构建的图对齐。

目前预印版图中标注疑似有误,\mathcal{L}_D 应该是限制类原的， \mathcal{L}_C 是拉进两个视图的，\mathcal{L}_G 是拉进视图和原型的。

图构建

为了将局部几何结构引入交互中，首先考虑局部输出特征表示 \boldsymbol{h} = [\boldsymbol{h}_1^\top,\boldsymbol{h}_2^\top,\ldots,\boldsymbol{h}_S^\top]^\top ，其中 \boldsymbol{h}_s\in\mathbb{R}^{\frac{d_h}S\times L} 表示等分后的第 S 个局部特征。选择预训练的 ViT 作为特征提取器 f_{\boldsymbol{\varphi}}(\cdot) : \mathcal{X} \to \mathbb{R}^{d_{h}\times L} 来探索 ViT 架构在 FSCIL 任务中的性能，其中 L 是 ViT 输出的 token 长度。我们设置一个可学习的矩阵 \mathbf{W}_{\boldsymbol{\theta}_1}\in \mathbb{R}^{d_h\times d_h}，由 \theta_1 参数化，来调整输出特征，表示为 \boldsymbol{\hbar} = \mathbb{L}(\boldsymbol{h}) := \mathbf{W}_{\boldsymbol{\theta}_1}\boldsymbol{h}。然后我们考虑 \boldsymbol{\hbar} 的局部信息。通过为每个局部特征 \boldsymbol{\hbar}_s 设置一个可学习的 MLP 模块 \mathcal{T}_{\theta_{2,s}}，由 \theta_{2,s} 参数化，继续对 \boldsymbol{\hbar} 进行变换，得到 \zeta=[\mathcal{T}_{\boldsymbol{\theta}_{2,1}}(\boldsymbol{\hbar}_1)^\top,\mathcal{T}_{\boldsymbol{\theta}_{2,2}}(\boldsymbol{\hbar}_2)^\top,\ldots,\mathcal{T}_{\boldsymbol{\theta}_{2,S}}(\boldsymbol{\hbar}_S)^\top]^\top

这里，为每个 \mathcal{T}_{\theta_{2,s}} 设置一个等分的隐藏维度，因此参数总数 \sum_{s=1}^S|\theta_{2,s}| 随着分区数量 S 的增加而减小。这并没有带来额外的参数存储负担，反而降低了模型的复杂度。（？此处个人存疑）

接下来对 token 维度上的 \zeta 进行平均，得到 \bar{\zeta}=[\bar{\zeta}_1^\top,\bar{\zeta}_2^\top,\ldots,\bar{\zeta}_S^\top]^\top\in\mathbb{R}^{d_\zeta}，其中 \bar{\zeta}_s\in\mathbb{R}^{\frac{d_\zeta}S}。使用 \bar{\zeta}，将原始的向量-向量的交互扩展到结合了局部特征之间的几何结构的图-图的交互。具体来说，将不同的局部特征 \bar{\zeta}_i 建模为具有局部邻接矩阵 \mathbf{A} 的加权图。\mathbf{A} 的元素满足 \mathbf{A}_{i,j} = 1/\exp(\|\bar{\zeta}_i -\bar{\zeta}_j\|_2)，反映不同局部特征之间的几何距离特征。

用于记忆交互的 G2G-GNN

利用构建的局部特征加权图，采用几种代表性的图神经网络模型 \mathcal{A}(\cdot):\mathbb{R}^{d_\zeta}\to\mathbb{R}^{d_\xi} 来捕获输出特征的几何结构。（GCN、GAT、GCNII、GGCN、GraphSage、GATv2）

每种模型具体的原理此处不做展开。将 GNN 集成到 G2G Interaction 模块后，函数 g_{\boldsymbol{\theta}} 可以统一表述如下：

其中 Ave 表示取平均值的操作，\mathcal{A}(\cdot)表示指定的 G2G-GNN。利用交互特征 \xi = g_θ(h)，设计了 G2G 交互来执行记忆检索。类似地，将交互特征 \xi 和原型 m 均等地划分为局部交互特征 \xi_s\in\mathbb{R}^{\frac{d_\xi}S} 和局部原型向量 m_s\in\mathbb{R}^{\frac{d_\xi}S} 。以同样的方式为它们构建局部邻接矩阵，分别表示为 \mathbf{A}^{\boldsymbol{\xi}} 和 \mathbf{A}^{\boldsymbol{m}}。利用上述符号，使用图级相异度度量 r(\cdot,\cdot)来同时衡量两者之间的特征差异和局部几何结构差异：

那么 G2G 记忆交互可以表示为：

为了在推理阶段赋予模型稳定的 G2G 检索能力，有必要在训练阶段鼓励紧密的 G2G 对齐。因此，我们在训练阶段引入了批量的 G2G 原型对比损失 \mathcal{L}_G，以促进 G2G 原型对齐并确保每个样本与同一批次中出现的其他类的原型保持较远的距离。给定一批样本 \mathcal{B} = \{(x_i, y_i)\}^{|\mathcal{B}|}_{i=1} 并将 \mathcal{Y} ^{\mathcal{B}} 表示为 \mathcal{B} 中观察到的所有类别， \mathcal{L}_G 定义为：

在每个阶段的训练之后，冻结与当前阶段中看到的类相对应的原型，并在后续阶段中保留其学习的结构。G2G 对齐可以对特征和类原型之间的位置关系进行更精确的建模。它只需使用一小部分样本进行排练即可准确恢复先前类别的特征，从而有效减轻灾难性遗忘。

对比增强 G2G 记忆交互

为了进一步增强 G2G 交互的稳定性，同时提高其小样本泛化能力，首先关注局部特征的几何结构。考虑到

1. 更清晰定义的局部几何结构原型导致更稳定的 G2G 对齐

2. 局部特征的解耦产生更丰富的特征表示，有助于防止阻碍泛化的局部特征崩溃。

因此，通过设计局部解耦损耗 \mathcal{L}_D 来引入局部图保存机制（LGP）机制，以对局部原型向量的结构施加额外的解耦约束：

对为了最大限度地利用样本信息并进一步增强 G2G 的小样本泛化能力，引入了对比增强 G2G 交互（CAG2G）机制。具体来说，对于增强前和增强后的样本 \boldsymbol{x} 和 \tilde{\boldsymbol{x}}，首先计算它们对应的 \zeta 和 \tilde{\zeta}。然后将它们连接起来以获得 \zeta^{[\boldsymbol{x},\tilde{\boldsymbol{x}}]} = [\zeta\|\tilde{\zeta}] \in \mathbb{R}^{2d_{\zeta}} 并构造连接局部特征的加权图。然后我们应用加权图注意力来获得交互特征 \xi^{[\boldsymbol{x},\tilde{\boldsymbol{x}}]}\in\mathbb{R}^{2d_\xi}。最后，我们提取相应的交互特征 \xi 和 \tilde{\xi}：

提出了一种局部图对比损失 \mathcal{L}_C 来在对齐过程中引入样本的对比信息：

其中 \tilde{\mathcal{B}} 表示数据增强后的批次 \mathcal{B}， \xi^i 和 \tilde{\xi}^i表示获得的样本 \boldsymbol{x}^i 和 \tilde{\boldsymbol{x}}^i 对应的交互特征。 CAG2G 有助于模型学习更鲁棒的特征表示，以增强其少样本泛化能力。

总体损失如下：

其中 λ 和 \eta 是超参数。为了确保受 LGP 约束的模型结构能够更稳​​定地对齐，我们在每个阶段中训练 I 次迭代的类原型，然后修复它们以减少训练期间因原型变化而导致的对齐不稳定。

实验与代码