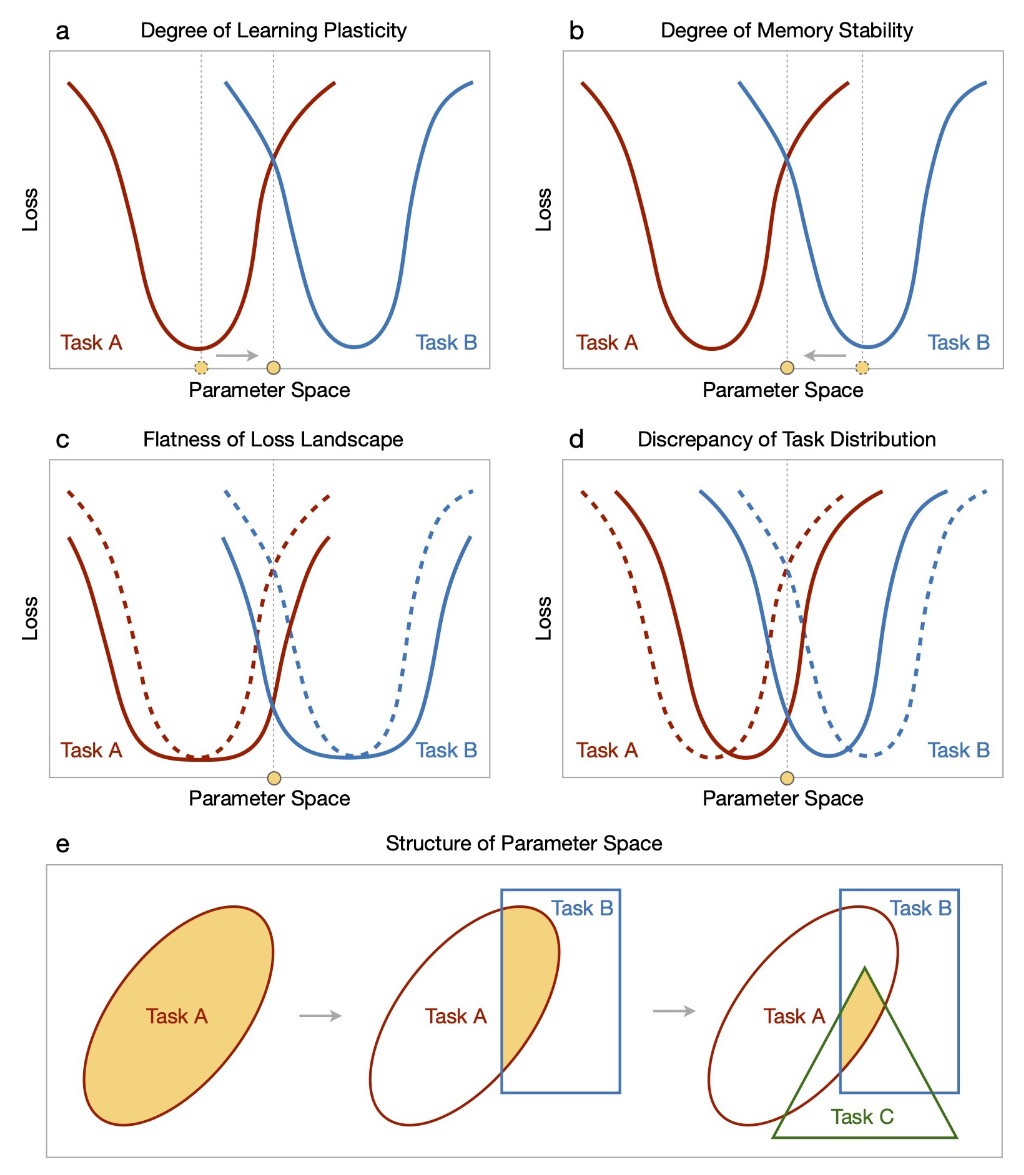
a，b：持续学习需要学习可塑性和记忆稳定性之间的适当平衡，其中任何一个过度都会影响整体表现。
c，d：当收敛的损失景观更平坦并且观察到的数据分布更相似时，适当平衡的解决方案可以更好地推广到任务序列。
在损失景观方面，收敛到具有更平坦损失景观的局部最小值将对适度的参数变化不太敏感，因此对新旧任务都有好处。具体的，对于给定的特定于任务的损失 \ell_t(\theta;\mathcal{D}_t) 及其经验最优解 \theta_{t}^{*}=\arg\min_{\theta}\ell_{t}(\theta;\mathcal{D}_{t})。当一个任务 i 需要容纳另一个任务 j 时，其性能的最大牺牲可以通过对 \ell_i(\theta;\mathcal{D}_i) 围绕 \theta^{*}_i 进行二阶泰勒展开来估计：
\begin{aligned} \ell_{i}(\theta_{j}^{*};\mathcal{D}_{i})& \approx\ell_{i}(\theta_{i}^{*};\mathcal{D}_{i})+(\theta_{j}^{*}-\theta_{i}^{*})^{\top}\nabla_{\theta}\ell_{i}(\theta;\mathcal{D}_{i})\big|_{\theta=\theta_{i}^{*}} \\ &+\frac12(\theta_j^*-\theta_i^*)^\top\nabla_\theta^2\ell_i(\theta;\mathcal{D}_i)\big|_{\theta=\theta_i^*}(\theta_j^*-\theta_i^*) \\ &\approx\ell_{i}(\theta_{i}^{*};\mathcal{D}_{i})+\frac{1}{2}\Delta\theta^{\top}\nabla_{\theta}^{2}\ell_{i}(\theta;\mathcal{D}_{i})\big|_{\theta=\theta_{i}^{*}}\Delta\theta \end{aligned}其中 Δθ := θ^*_j − θ^*_i 且\left.\nabla_{\theta}\ell_{i}(\theta;\mathcal{D}_{i})\right|_{\theta=\theta_{i}^{\star}}\approx0。那么，任务 i 的性能下降上限为：
\ell_i(\theta_j^*;\mathcal{D}_i)-\ell_i(\theta_i^*;\mathcal{D}_i)\leq\frac{1}{2}\lambda_i^{max}\|\Delta\theta\|^2\tag{1}其中 \lambda_i^{max} 是 Hessian 矩阵 \left.\nabla_{\theta}^2\ell_{i}(\theta;\mathcal{D}_{i})\right|_{\theta=\theta_{i}^{\star}} 的最大特征值。注意，任务 i 和 j 的顺序可以是任意的，即式 (1) 同时展示了前向和后向的差值。因此，经验最优解 \theta^{*}_i 对参数变化的鲁棒性与 \lambda_i^{max} 密切相关， \lambda_i^{max} 是描述损失景观平坦度的常用指标。
在数据分布方面，因为性能下降的上限还取决于每个任务的经验最优解的差异，即任务分布的差异。每个任务的泛化误差可以通过协同任务得到改善，但随着竞争任务而恶化，在共享解决方案中平等地学习所有任务往往会损害每个任务的性能。而且当模型参数不被所有任务共享时（例如，使用多头输出层），任务相似性的增加反而可能会导致更多的遗忘（由于输出头对于各个任务是独立的，因此区分两个相似的解决方案变得更加困难）。任务相似性的复杂影响表明模型架构对于协调任务共享和特定任务组件的重要性。
e：参数空间的结构决定了找到理想解决方案的复杂性和可能性。黄色区域表示各个任务共享的可行参数空间，随着更多增量任务的引入，该空间趋于狭窄且不规则。
使用共享解决方案学习所有增量任务相当于在受限参数空间中学习每个新任务，从而防止所有旧任务的性能下降。这种经典的持续学习问题已被证明一般来说是NP难问题。
持续学习的理想解决方案应该提供适当的稳定性-可塑性权衡和足够的任务内/任务间泛化性。
The Ideal Continual Learner: An Agent That Never Forgets 在假设所有任务共享一个具有均匀收敛的全局最小的优化器的条件下，给出了理想持续学习器的泛化准确率边界。